设椭圆 过点 ,且左焦点为
(Ⅰ)求椭圆
的方程;
(Ⅱ)当过点
的动直线
与椭圆
相交与两不同点
时,在线段
上取点
,满足
,证明:点
总在某定直线上.
已知等差数列 的前n项和为
的前n项和为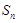 ,且
,且 .
.
(1)求数列 的通项公式与
的通项公式与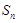 ;
;
(2)若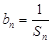 ,求数列
,求数列 的前n项和.
的前n项和.
已知 为实数,用[
为实数,用[ ]表示不超过
]表示不超过 的最大整数,例如
的最大整数,例如 ,
, ,
, .对于函数
.对于函数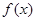 ,若存在
,若存在 且
且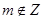 ,使得
,使得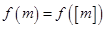 ,则称函数
,则称函数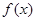 是
是 函数.
函数.
(Ⅰ)判断函数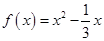 ,
, 是否是
是否是 函数;(只需写出结论)
函数;(只需写出结论)
(Ⅱ)已知 ,请写出
,请写出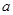 的一个值,使得
的一个值,使得 为
为 函数,并给出证明;
函数,并给出证明;
(Ⅲ)设函数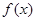 是定义在
是定义在 上的周期函数,其最小周期为
上的周期函数,其最小周期为 .若
.若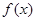 不是
不是 函数,求
函数,求 的最小值.
的最小值.
已知数列{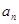 }的各项均不为0,其前
}的各项均不为0,其前 项和为Sn,且满足
项和为Sn,且满足 =
= ,
,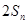 =
=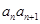 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求{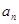 }的通项公式;
}的通项公式;
(Ⅲ)若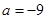 ,求
,求 的最小值.
的最小值.
已知函数 .
.
(Ⅰ)若曲线 在点(0,1)处切线的斜率为-3,求函数
在点(0,1)处切线的斜率为-3,求函数 的单调区间;
的单调区间;
(Ⅱ)若函数 在区间[-2,
在区间[-2, ]上单调递增,求
]上单调递增,求 的取值范围.
的取值范围.
如图,在四边形ABCD中,AB=8,BC=3,CD=5,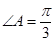 ,
, .
.
(Ⅰ)求BD的长;
(Ⅱ)求 的面积.
的面积.