已知二次函数 同时满足:①不等式
同时满足:①不等式 ≤0的解集有且只有一个元素;②在定义域内存在
≤0的解集有且只有一个元素;②在定义域内存在 ,使得不等式
,使得不等式 成立,设数列{
成立,设数列{ }的前
}的前 项和
项和 .
.
(1)求函数 的表达式;
的表达式;
(2) 设各项均不为0的数列{ }中,所有满足
}中,所有满足 的整数
的整数 的个数称为这个数列{
的个数称为这个数列{ }的变号数,令
}的变号数,令 (
(
 ),求数列{
),求数列{ }的变号数;
}的变号数;
(3)设数列{ }满足:
}满足: ,试探究数列{
,试探究数列{ }是否存在最小项?若存在,求出该项,若不存在,说明理由.
}是否存在最小项?若存在,求出该项,若不存在,说明理由.
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示(在答题卡上).
(Ⅰ)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(Ⅱ)为了能选拔出最优秀的学生,该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求第四组至少有一名学生被考官A面试的概率?
设有关于 的一元二次方程
的一元二次方程 .
.
(1)若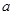 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若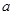 是从区间[0,3]中任取的一个数,
是从区间[0,3]中任取的一个数, 是从区间[0,2]中任取的一个数,求上述方程有实根的概率;
是从区间[0,2]中任取的一个数,求上述方程有实根的概率;
现有8名奥运会志愿者,其中志愿者 通晓日语,
通晓日语, 通晓俄语,
通晓俄语,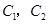 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(Ⅰ)求 被选中的概率;
被选中的概率;
(Ⅱ)求 和
和 不全被选中的概率.
不全被选中的概率.
如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以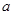 表示.已知甲、乙两个小组的数学成绩的平均分相同.
表示.已知甲、乙两个小组的数学成绩的平均分相同.
(1)求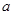 的值;
的值;
(2)求乙组四名同学数学成绩的方差;
(3)分别从甲、乙两组同学中各随机选取一名同学,求这两名同学数学成绩之差的绝对值为3的概率.
(注:方差 ,其中
,其中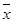 为
为 ,
,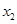 ,…,
,…, 的平均数)
的平均数)
已知函数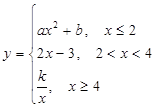 的图象如图所示.
的图象如图所示.
(1)求函数的解析式;
(2)完成下面的程序,并根据程序画出其程序框图.
INPUT“x=”;x
IF ①THEN
IF ②THEN
y=2*x-3
ELSE
y=k/x
END IF
ELSE
y=a*x^2+b
END IF
PRINT “y=”;y
END