已知关于x,y的方程C: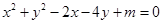
(1)若方程C表示圆,求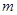 的取值范围;
的取值范围;
(2)若圆C与圆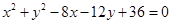 外切,求
外切,求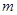 的值.
的值.
(本小题满分12分)如图,四棱锥 的底面是正方形,
的底面是正方形, ⊥底面
⊥底面 ,点
,点 在棱
在棱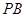 上.
上.
(Ⅰ)求证:平面 ⊥平面
⊥平面 ;
;
(Ⅱ)当 且
且 为
为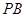 的中点时,求
的中点时,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)已知各项都不相等的等差数列{an}的前六项和为60,且a6为a1和a21的等比中项.
(1)求数列{an}的通项公an及前n项和Sn;
(2)若数列{bn}满足bn+1-bn=an(n∈N*),且b1=3,求数列{}的前n项和Tn.
(本小题满分12分)在△ABC中,内角A,B,C的对边分别是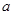 ,
,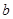 ,
,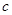 ,已知
,已知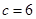 ,sinA-sinC=sin(A-B).
,sinA-sinC=sin(A-B).
(Ⅰ)求B;
(Ⅱ)若b=2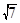 ,求△ABC的面积。
,求△ABC的面积。
(本小题满分14分)如图所示,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的右侧),且|MN|=3,已知椭圆D: +
+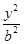 =1(a>b>0)的焦距等于2|ON|,且过点(
=1(a>b>0)的焦距等于2|ON|,且过点(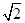 ,
, ).
).
(1)求圆C和椭圆D的方程;
(2)若过点M斜率不为零的直线l与椭圆D交于A、B两点,求证:直线NA与直线NB的倾斜角互补.
(本小题满分13分)已知数列 的前
的前 项和为
项和为 ,且
,且 =
=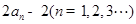 ,数列
,数列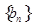 中,
中, ,点
,点 在直线
在直线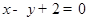 上.
上.
(1)求数列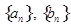 的通项
的通项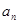 和
和 ;
;
(2)设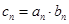 ,求数列
,求数列 的前n项和
的前n项和 ,并求满足
,并求满足 的最大正整数
的最大正整数 .
.