如图, 椭圆C: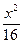 +
+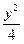 =1的右顶点是A,上下两个顶点分别为B、D,四边形DAMB是矩形(O为坐标原点)
=1的右顶点是A,上下两个顶点分别为B、D,四边形DAMB是矩形(O为坐标原点) ,点E、P分别是线段OA、AM的中点。
,点E、P分别是线段OA、AM的中点。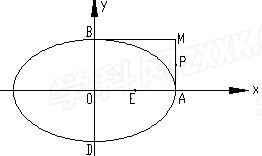
(1)求证:直线DE与直线BP的交点在椭圆C上.
(2)过点B的直线l1、l2与椭圆C分别交于R、S(不同于B点),且它们的斜率k1、k2满足k1*k2=-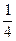 ,求证:直线RS过定点,并求出此定点的坐标。
,求证:直线RS过定点,并求出此定点的坐标。
【原创】(本小题满分12分)已知等差数列 ,
, 为其前
为其前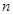 项和,
项和,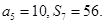
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列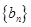 的前
的前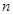 项和
项和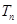
【原创】(本小题满分12分)设函数 ,其中
,其中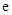 为自然对数的底数.
为自然对数的底数.
(Ⅰ) 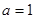 时,求曲线
时,求曲线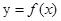 在点
在点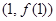 处的切线方程;
处的切线方程;
(Ⅱ)函数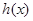 是
是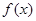 的导函数,求函数
的导函数,求函数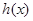 在区间
在区间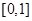 上的最小值.
上的最小值.
【原创】(本小题满分14分)已知数列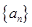 与
与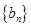 满足
满足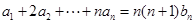 ,
,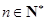 .
.
(Ⅰ)若
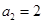 ,求
,求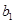 ,
,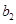 ;
;
(Ⅱ)若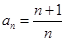 ,求证:
,求证: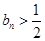 ;
;
(Ⅲ)若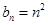 ,求数列
,求数列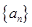 的通项公式.
的通项公式.
【原创】(本小题满分12分)如图,在三棱锥 中,
中, 底面ABC,
底面ABC, ,AP=AC, 点
,AP=AC, 点 ,
, 分别在棱
分别在棱 上,且BC//平面ADE.
上,且BC//平面ADE.
(Ⅰ)求证:DE⊥平面 ;
;
(Ⅱ)若PC⊥AD,且三棱锥 的体积为8,求多面体ABCED的体积.
的体积为8,求多面体ABCED的体积.
【改编】(本小题满分12分)已知某校 四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从
四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从 四个社团的学生当中随机抽取10名学生参加问卷调查.
四个社团的学生当中随机抽取10名学生参加问卷调查.
(Ⅰ)从 四个社团中各抽取多少人?
四个社团中各抽取多少人?
(Ⅱ)在社团 所抽取的学生总数中,任取2个,求
所抽取的学生总数中,任取2个,求 社团中各有1名学生的概率.
社团中各有1名学生的概率.