（文）某企业原有产品每年投入x万元,所获年利润为
(万元)，对开发的新产品,每年投入x万元,所获年利润为
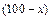(万元)，新产品开发用两年时间完成，这两年，每年从100万元生产准备资金中拿出80万元投入新产品开发，从第三年开始这100万元可随意分配且全部用于新旧产品的生产投入.为解决资金缺口，第一年初向银行贷款1000万元，年利率5.5%（不计复利，即先一年利息不计入下一年本金）.（1）第五年底一次性向银行还本息多少万元？（2）从新产品开发的第三年起，新旧产品各投入多少万元年利润最大，最大利润是多少？（3）从新旧产品生产五年的最高利润总和中拿出70%来能否还清贷款？
甲、乙两人解关于
的方程：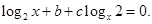
甲写错了常数b，得到根为
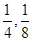，乙写错了常数c，得到根为
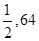.求方程的真正根。
已知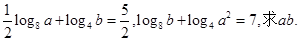
(本小题满分14分)为了解初三学生女生身高情况，某中学对初三女生身高进行了一次抽样调查，根据所得数据整理后列出了频率分布表如下：
组 别频数频率
145.5～149.5 1 0.02
149.5～153.5 4 0.08
153.5～157.5 22 0.44
157.5～161.5 13 0.26
161.5～165.5 8 0.16
165.5～169.5m n
合 计 M N
（1）求出表中所表示的数m,n,M,N分别是多少？
（2）画出频率分布直方图和频率分布折线图.
（3）若要从中再用分层抽样方法抽出10人作进一步调查，则身高在[153.5，161.5）范围内的应抽出多少人？
（4）根据频率分布直方图，分别求出被测女生身高的众数，中位数和平均数？（结果保留一位小数）
(本题满分13分)已知关于x的二次函数
（1）设集合
和
，从集合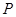
中随机取一个数作为
，从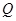
中随机取一个数作为
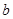，求函数
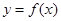在区间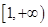
上是增函数的概率；
（2）设点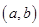
是区域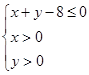
内的随机点，求函数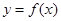在区间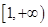上是增函数的概率.
(本小题满分14分)
某班甲、乙两名同学参加l00米达标训练，在相同条件下两人l0次训练的成绩(单位：秒)如下：
(I)请画出适当的统计图（茎叶图或频率分布直方图）；如果从甲、乙两名同学中选一名参加学校的100米比赛，从成绩的稳定性方面考虑，选派谁参加比赛更好，并说明理由(不用计算，可通过统计图直接回答结论)．
(Ⅱ)从甲、乙两人的10次成绩中各随机抽取一次，求抽取的成绩中至少有一个不高于 12．8秒的概率．
(III)经过对甲、乙两位同学的若干次成绩的统计，甲、乙的成绩都均匀分布在[11．5，14．5]之间，
现甲、乙比赛一次，求甲、乙成绩之差的绝对值小于0．8秒的概率．