甲、乙两人解关于 的方程:
的方程: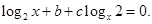 甲写错了常数b,得到根为
甲写错了常数b,得到根为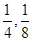 ,乙写错了常数c,得到根为
,乙写错了常数c,得到根为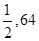 .求方程的真正根。
.求方程的真正根。
(本小题满分10分)
已知 的面积是30,内角
的面积是30,内角
 、
、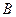 、
、 所对边长分别为
所对边长分别为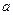 、
、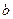 、
、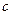 ,
,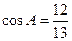 .
.
(1)求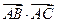 ;(2)若
;(2)若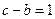 ,求
,求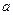 的值.
的值.
(本小题满分12分)已知函数 .
.
(Ⅰ)设 ,讨论
,讨论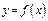 的单调性;
的单调性;
(Ⅱ)若对任意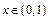 恒有
恒有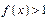 ,求
,求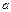 的取值范围.
的取值范围.
(本小题满分12分)已知函数f(x)=x3+ax2+bx+c在x=- 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值与函数f(x)的单调区间;
(2)xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围.
(本小题满分12分)已知函数f(x)=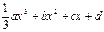 ,其中a , b , c是以d为公差的等差数列,且a>0,d>0.设
,其中a , b , c是以d为公差的等差数列,且a>0,d>0.设 [1-
[1- ]上,
]上, ,在
,在
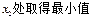 ,将点
,将点 A, B, C,
A, B, C,
(Ⅰ)求
(II)若⊿ABC有一边平行于x轴,且面积为 ,求a ,d的值.
,求a ,d的值.
(本小题满分12分)设函数
 其中
其中
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ) 讨论 的极值.
的极值.