已知F1、F2是椭圆c1：
(a>b>0)的左、右焦点，A为右顶点，P为椭圆c1上任意一点，且
最大值的取值范围是[c2,3c2]，c2=a2-b2.（1）求椭圆c1离心率e的取值范围；（2）设双曲线c2以椭圆c1焦点为顶点，顶点为焦点，B是双曲线c2在第一象限上任意一点，当椭圆c1离心率e取得最小值时，问是否存在正常数λ使∠BAF1=λ∠BF1A恒成立？若存在，求出λ值；若不存在，请说明理由.
.(本题满分12分)
如图，四棱锥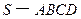
的底面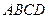
是正方形，侧面
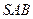是等腰三角形且垂直于底面，
，
，
、
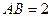分别是
、
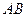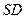的中点。
（1）求证：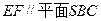
；
（2）求二面角
的大小。
(本题满分12分)
设p:实数x满足
,其中
,命题
实数
满足
.
(Ⅰ)若
且
为真，求实数的取值范围；
(Ⅱ)若
是
的充分不必要条件,求实数的取值范围.
(本题满分10分)
如图，要计算西湖岸边两景点
与
的距离，由于地形的限制，需要在岸上选取
和
两点，现测得
，
，
，
，
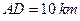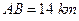，求两景点与的距离（精确到0.1km）．参考数据：
(本小题满分
12分)
已知椭圆C:
（a＞b＞0）的离心率为
短轴一个端点到右焦点的
距离为
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C交于A、B两点，坐标原点O到直线l的距离为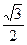
，求△AOB面积的
最大值.
本小题满分12分)
已知
函数f (x)=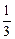
x3+ ax2－bx(a, b∈R) .
(1)若y=f (x)图象上的点(1，－
)处的切线斜率为－4
，求y=f (x)的极大值；
(2)若y=f (x)在区间[－1，2]上是单调减函数，求a + b的最小值.