(本小题满分12分)在正方体 中,棱长
中,棱长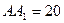 .
.
(1)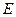 为棱
为棱 的中点,求证:
的中点,求证: ;
;
(2)求二面角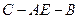 的大小;
的大小;
(3)求点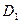 到平面
到平面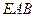 的距离.
的距离.
已知函数
(1)设ω>0为常数,若y=f(ωx)在区间[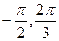 ]上是增函数,求ω的取值范围。
]上是增函数,求ω的取值范围。
(2)求
已知函数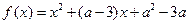 (a为常数)
(a为常数)
(1)如果对任意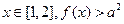 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(2)设实数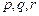 满足:
满足: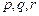 中的某一个数恰好等于a,且另两个恰为方程
中的某一个数恰好等于a,且另两个恰为方程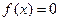 的两实根,判断①
的两实根,判断①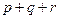 ,②
,②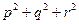 ,③
,③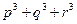 是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数
是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数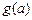 ,并求
,并求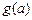 的最小值;
的最小值;
(3)对于(2)中的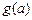 ,设
,设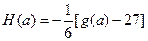 ,数列
,数列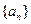 满足
满足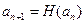
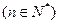 ,且
,且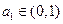 ,试判断
,试判断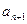 与
与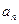 的大小,并证明。
的大小,并证明。
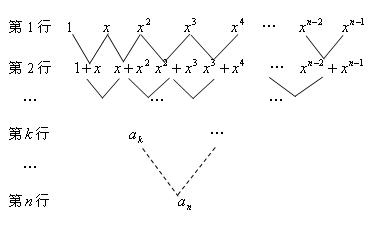
下图是一个三角形数阵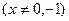 ,从第二行起每个数都等于它肩上两个数的和,第
,从第二行起每个数都等于它肩上两个数的和,第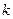 行的第一个数为
行的第一个数为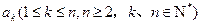
(Ⅰ)写出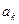 关于
关于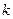 的表达式:
的表达式: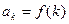 ,不需证明。
,不需证明。
(Ⅱ)求第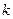 行中所有数的和
行中所有数的和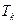 ;
;
(Ⅲ)当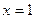 时,求数阵中所有
时,求数阵中所有
数的和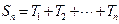 .
.
右图的程序可产生一系列随机数,其工作原理如下:
①从集合D中随机抽取1个数作为自变量 输入;
输入;
②从函数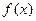 与
与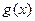 中随机选择一个作为
中随机选择一个作为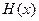 进行计算;
进行计算;
③输出函数值 。
。
若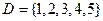 ,
,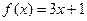 ,
,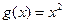 ,
,
(1)求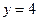 的概率;
的概率;
(2)将程序运行4次,求恰好有2次的输出结果是奇数的概率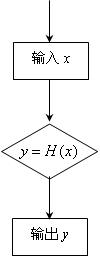
设函数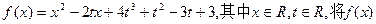 的最小值记为g(t).
的最小值记为g(t).
(1)求g(t)的表达式;
(2)讨论g(t)在区间[-1,1]内的单调性;
(3)当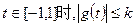 恒成立,其中k为正数,求k的取值范围.
恒成立,其中k为正数,求k的取值范围.