如图所示,有两条相交成 角的直路
角的直路 ,
,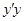 ,交点是
,交点是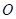 ,甲、乙分别在
,甲、乙分别在 ,
, 上,起初甲离
上,起初甲离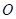 点
点 km,乙离
km,乙离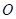 点
点 km,后来两人同时用每小时
km,后来两人同时用每小时 km的速度,甲沿
km的速度,甲沿 的方向,乙沿
的方向,乙沿 的方向步行.
的方向步行.
⑴起初,两人的距离是多少?
⑵用包含 的式子表示
的式子表示 小时后两人的距离;
小时后两人的距离;
⑶什么时候两人的距离最短?
设函数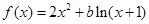 ,其中
,其中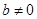 .
.
(1)当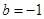 时,求在曲线
时,求在曲线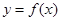 上一点
上一点 处的切线方程;
处的切线方程;
(2)求函数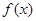 的极值点。
的极值点。
已知数列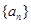 的前
的前 项和为
项和为 ,且
,且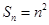 .数列
.数列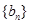 为等比数列,且
为等比数列,且 ,
, .
.
(1)求数列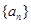 ,
,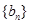 的通项公式;
的通项公式;
(2)若数列 满足
满足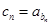 ,求数列
,求数列 的前
的前 项和
项和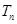 .
.
某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示。
(1)请根据图中所给数据,求出 的值;
的值;
(2)从成绩在[50,70)内的学生中随机选3名学生,求这3名学生的成绩都在[60,70)内的概率;
(3)为了了解学生本次考试的失分情况,从成绩在[50,70)内的学生中随机选取3人的成绩进行分析,用X表示所选学生成绩在[ 60,70)内的人数,求X的分布列和数学期望.
已知函数 .
.
(1)若 ,求
,求 的最大值及此时相应的
的最大值及此时相应的 的值;
的值;
(2)在△ABC中, 、b、c分别为角A、B、C的对边,若
、b、c分别为角A、B、C的对边,若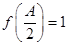 ,b =l,
,b =l,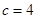 ,求
,求 的值.
的值.
已知向量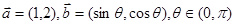 。
。
(1)若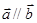 ,求
,求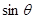 及
及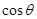 ;
;
(2)若 ,求
,求 。
。