某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示。
(1)请根据图中所给数据,求出 的值;
的值;
(2)从成绩在[50,70)内的学生中随机选3名学生,求这3名学生的成绩都在[60,70)内的概率;
(3)为了了解学生本次考试的失分情况,从成绩在[50,70)内的学生中随机选取3人的成绩进行分析,用X表示所选学生成绩在[ 60,70)内的人数,求X的分布列和数学期望.
已知椭圆G的中心在坐标原点,长轴在x轴上,离心率为 ,两个焦点分别为
,两个焦点分别为
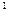 和
和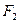 ,椭圆G上一点到
,椭圆G上一点到 和
和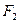 的距离之和为12.
的距离之和为12.
圆 :
: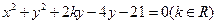 的圆心为点
的圆心为点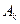 .
.
(1)求椭圆G的方程;(2)求
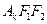 面积;(3)问是否存在圆
面积;(3)问是否存在圆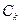 包围椭圆G?请说明理由.
包围椭圆G?请说明理由.
已知椭圆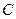 的中心为直角坐标系
的中心为直角坐标系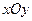 的原点,焦点在
的原点,焦点在 轴上,它的一个项点到两个焦点的距离分别是7和1.
轴上,它的一个项点到两个焦点的距离分别是7和1.
(I)求椭圆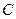 的方程;
的方程;
(II)若 为椭圆
为椭圆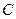 的动点,
的动点,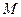 为过
为过 且垂直于
且垂直于 轴的直线上的点,
轴的直线上的点, (e为椭圆C的离心率),求点
(e为椭圆C的离心率),求点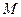 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
(满分14分)在斜四棱柱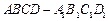 中,已知底面
中,已知底面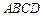 是边长为4的菱形,
是边长为4的菱形,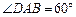 ,且点
,且点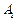 在面
在面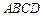 上的射影是底面对角线
上的射影是底面对角线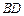 与AC的交点O,设点E是
与AC的交点O,设点E是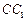 的中点,
的中点,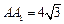 .
.
(Ⅰ) 求证:四边形 是矩形;
是矩形;
(Ⅱ) 求二面角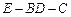 的大小;
的大小;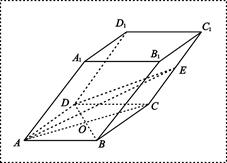 (Ⅲ) 求四面体
(Ⅲ) 求四面体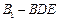 的体积.
的体积.
如图,在棱长为1的正方体 中,
中,
(I)在侧棱 上是否存在一个点P,使得直线
上是否存在一个点P,使得直线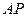 与平面
与平面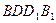 所成角的正切值为
所成角的正切值为
 ;(Ⅱ)若P是侧棱
;(Ⅱ)若P是侧棱 上一动点,在线段
上一动点,在线段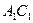 上是否存在一个定点
上是否存在一个定点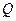 ,使得
,使得 在平面
在平面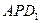 上的射影垂直于
上的射影垂直于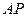 .并证明你的结论.
.并证明你的结论.
正方形ABCD边长为4,点E是边CD上的一点,
将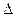 AED沿AE折起到
AED沿AE折起到 的位
的位 置时,有平面
置时,有平面
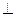 平面ABCE,
平面ABCE,
并且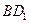
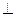
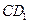 (如图)
(如图)
(I)判断并证明E点的具体位置;(II) 求点D/到平面ABCE的距离.
求点D/到平面ABCE的距离.