(本题满分12分) 已知函数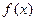
=
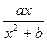，在x=1处取得极值为2.（1）求函数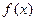的解析式；（2）若函数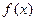在区间（m，2m＋1）上为增函数，求实数m的取值范围；（3）若P（x0，y0）为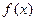=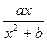图象上的任意一点，直线l与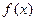=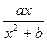的图象相切于点P，求直线l的斜率的取值范围.
圆锥曲线上任意两点连成的线段称为弦。若圆锥曲线上的一条弦垂直于其对称轴，我们将该弦称之为曲线的垂轴弦。已知点
、
是圆锥曲线C
上不与顶点重合的任意两点，
是垂直于
轴的一条垂轴弦，直线
分别交轴于点
和点
。
（1）试用
的代数式分别表示
和
；
（2）若C的方程为
（如图），求证：
是与和点
位置无关的定值；
（3）请选定一条除椭圆外的圆锥曲线C，试探究和经过某种四则运算（加、减、乘、除），其
结果是否是与和点位置无关的定值，写出你的研究结论并证明。
各项均为正数的数列
的前
项和为
，满足
（1）求数列的通项公式；
（2）若数列
满足
，
数列
满足
，数列的前
项和为
，求；
（3）若数列
，甲同学利用第（2）问中的，试图确定
的值是否可以等于2011？为此，他设计了一个程序
（如图），但乙同学认为这个程序如果被执行会是一个“死循环”（即程序会永远循环下去，而无法结束），你是否同意乙同学的观点？请说明理由。
已知关于
的不等式
，其中
。
（1）求上述不等式的解；
（2）是否存在实数
，使得上述不等式的解集
中只有有限个整数？若存在
，求出使得中整数个数最少的的值；若不存在，请说明理由。
设函数
。
（1）当
时，求函数
的最小值；
（2）当
时，试判断函数的单调性，并证明。
在
中，角
、
、
的对边分别为
、
、
，且
。
（1）求
的值；
（2）若
，且
，求和的值