(本小题满分13分) 近段时间我国北方严重缺水, 某城市曾一度取消洗车行业. 时间久了,车 容影响了市容市貌. 今年该市决定引进一
容影响了市容市貌. 今年该市决定引进一 种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车. 污水净化器的价格是每台90万元,全市统一洗车价格为每辆每次8元. 该市今年的汽车总量是80000辆,预计今后每年汽车数量将增加2000辆.洗车行A经过测算,如果全市的汽车总量是x,那么一年内在该洗车行洗车的平均辆次是
种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车. 污水净化器的价格是每台90万元,全市统一洗车价格为每辆每次8元. 该市今年的汽车总量是80000辆,预计今后每年汽车数量将增加2000辆.洗车行A经过测算,如果全市的汽车总量是x,那么一年内在该洗车行洗车的平均辆次是 ,该洗车行每年的其他费用是20000元. 问:洗车行A从今年开始至少经
,该洗车行每年的其他费用是20000元. 问:洗车行A从今年开始至少经 过多少年才能收回购买净化器的成本?(注:洗车行A买一台污水净化器就能满
过多少年才能收回购买净化器的成本?(注:洗车行A买一台污水净化器就能满 足洗车净水需求)
足洗车净水需求)
设
,函数
.
(1)求
的单调区间;
(2)证明
在
上仅有一个零点;
(3)若曲线
在点
处的切线与
轴平行,且在点
处的切线与直线
平行,(
是坐标原点),证明:
.
如图,三角形
所在的平面与长方形
所在的平面垂直,
,
,
,点
是
的中点,点
、
分别在线段
、
上,且
,
.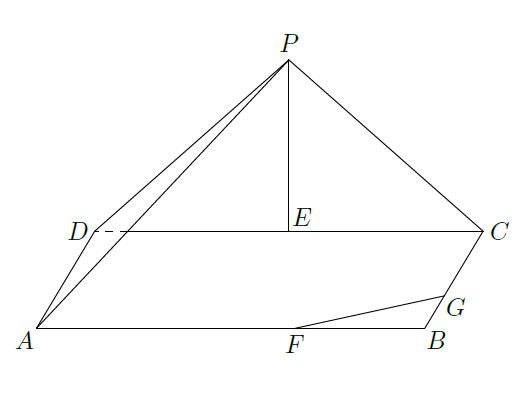
(1)证明:
;
(2)求二面角
的正切值;
(3)求直线
与直线
所成角的余弦值.
某工厂36名工人年龄数据如图: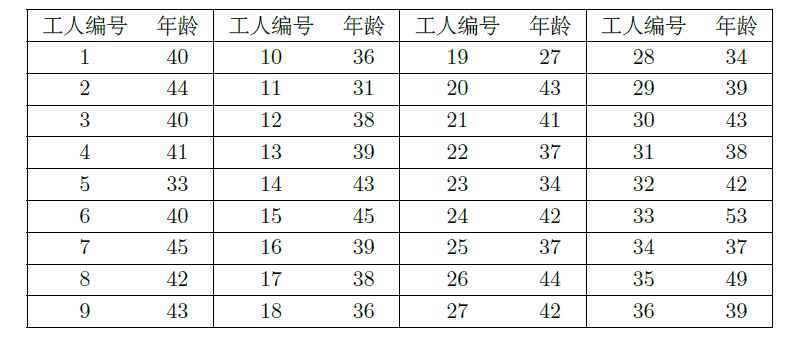
(1)用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
(2)计算(1)中样本的均值
和方差
;
(3)36名工人中年龄在
﹣
和
+
之间有多少人?所占百分比是多少(精确到
)?
在平面直角坐标系 中,已知向量 .
(1)若
,求
的值;
(2)若
与
的夹角为
,求
的值.
已知集合
,
,令
表示集合
所含元素的个数.
(1)写出
的值;
(2)当
时,写出
的表达式,并用数学归纳法证明.