(本小题满分12分)如图,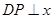 轴,点
轴,点 在
在 的延长线上,且
的延长线上,且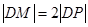 ,当点
,当点 在圆
在圆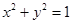 上运动时.
上运动时.
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 作圆
作圆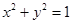 的切线
的切线 交曲线
交曲线 于
于 ,
, 两点,求
两点,求 面积
面积 的最大值和相应的点
的最大值和相应的点 的坐标.
的坐标.
在圆 上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹方程,指出轨迹是什么?并求出该轨迹的焦点和离心率.
上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹方程,指出轨迹是什么?并求出该轨迹的焦点和离心率.
设函数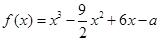 .
.
(1)求函数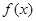 的单调区间.
的单调区间.
(2)若方程 有且仅有三个实根,求实数
有且仅有三个实根,求实数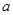 的取值范围.
的取值范围.
已知命题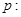 方程
方程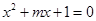 有两个不等的正实数根;命题
有两个不等的正实数根;命题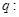 方程
方程 无实数根。若“
无实数根。若“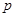 或
或 ”为真命题,求
”为真命题,求 的取值范围.
的取值范围.
(本小题满分13分)已知函数 .
.
(1)若对于区间 内的任意
内的任意 ,总有
,总有 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(2)若函数 在区间
在区间 内有两个不同的零点
内有两个不同的零点 ,求:
,求:
①实数 的取值范围;②
的取值范围;② 的取值范围.
的取值范围.
(本小题满分13分)已知数列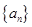 中,
中, ,其前
,其前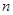 项和
项和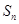 满足
满足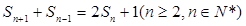 .
.
(1)求证:数列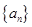 为等差数列,并求
为等差数列,并求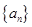 的通项公式;
的通项公式;
(2)设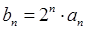 ,求数列
,求数列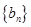 的前
的前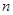 项和
项和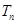 ;
;
(3)设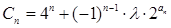 (
(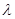 为非零整数,
为非零整数,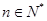 ),是否存在确定
),是否存在确定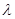 的值, 使得对任意
的值, 使得对任意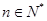 ,有
,有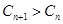 恒成立.若存在求出
恒成立.若存在求出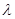 的值,若不存在说明理由。
的值,若不存在说明理由。