已知 直线
直线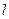 与函数
与函数 、
、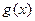 的图象都相切,且与函数
的图象都相切,且与函数 的图象的切点的横坐标为1.(1)求直线
的图象的切点的横坐标为1.(1)求直线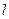 的方程和
的方程和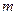 的值; (2)若
的值; (2)若
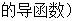 ,求函数
,求函数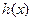 的最大值;(3)当
的最大值;(3)当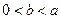 时,求证:
时,求证:
(本小题满分10分)设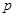 :
: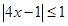 ;
;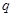 :
: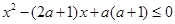 .若
.若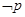 是
是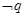 的必要而不充分条件,求实数
的必要而不充分条件,求实数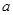 的取值范围.
的取值范围.
【原创】在复平面内,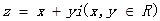 ,
,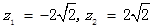 ,
,
(1)若 ,求点
,求点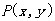 的轨迹
的轨迹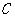 方程;
方程;
(2)过复数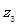 对应的点M作斜率为1直线
对应的点M作斜率为1直线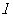 与曲线
与曲线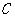 交于A、B两点,求线段AB的长度.
交于A、B两点,求线段AB的长度.
(本小题满分10分)选修4—5:不等式选讲
已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.
(1)当a=-2时,求不等式f(x)<g(x)的解集;
(2)设a>-1,且当x∈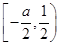 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围.
(本小题满分10分)选修4—4:坐标系与参数方程
已知曲线C1的参数方程为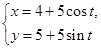 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
(本小题满分10分)选修4—1:几何证明选讲
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.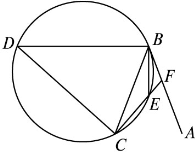
(1)证明:DB=DC;
(2)设圆的半径为1,BC=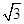 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.