(本小题满分13分)设函数 .
. (Ⅰ)求函数
(Ⅰ)求函数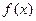 的单调区间;(Ⅱ)若常数
的单调区间;(Ⅱ)若常数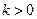 ,求不等式
,求不等式 的解集.
的解集.
(本小题满分12分)在 年
年 月,某市进行了“居民幸福度”的调查,某师大附中学生会组织部分同学,用“
月,某市进行了“居民幸福度”的调查,某师大附中学生会组织部分同学,用“ 分制”随机调查“狮子山”社区人们的幸福度.现从调查人群中随机抽取
分制”随机调查“狮子山”社区人们的幸福度.现从调查人群中随机抽取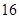 名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).
名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).
(1)若幸福度不低于 分,则称该人的幸福度为“极幸福”,求从这
分,则称该人的幸福度为“极幸福”,求从这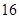 人中随机选取
人中随机选取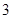 人,至
人,至
多有 人是“极幸福”的概率;
人是“极幸福”的概率;
(2)以这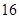 人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选
人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选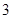 人,记
人,记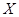
表示抽到“极幸福”的人数,求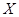 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)已知向量 ,函数
,函数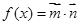 .
.
(1)求函数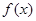 的单调递增区间;
的单调递增区间;
(2)在 中,角
中,角 的对边分别为
的对边分别为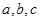 ,若
,若 ,
,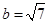 ,
,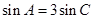 ,求
,求 的面积.
的面积.
(本小题满分12分) 已知 为等比数列,其中
为等比数列,其中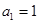 ,且
,且 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)设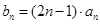 ,求数列
,求数列 的前
的前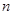 项和
项和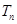 .
.
(本小题满分16分)己知函数 
(1)若  ,求函数
,求函数 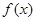 的单调递减区间;
的单调递减区间;
(2)若关于x的不等式  恒成立,求整数 a的最小值:
恒成立,求整数 a的最小值:
(3)若  ,正实数
,正实数 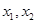 满足
满足 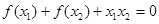 ,证明:
,证明: 
(本小题满分16分)在数列 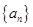 中,已知
中,已知  ,
, 为常数.
为常数.
(1)证明: 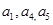 成等差数列;
成等差数列;
(2)设 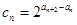 ,求数列 的前n项和
,求数列 的前n项和 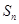 ;
;
(3)当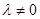 时,数列
时,数列 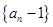 中是否存在三项
中是否存在三项 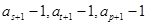 成等比数列,且
成等比数列,且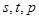 也成等比数列?若存在,求出
也成等比数列?若存在,求出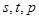 的值;若不存在,说明理由.
的值;若不存在,说明理由.