 某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试. 假设某学生每次通过测试的概率都是
某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试. 假设某学生每次通过测试的概率都是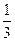 ,每次测试通过与否互相独立. 规定:若前4次都没有通过测试,则第5次不能参加测试.
,每次测试通过与否互相独立. 规定:若前4次都没有通过测试,则第5次不能参加测试. (1)求该学生恰好经过4次测试考上大学的概率;
(1)求该学生恰好经过4次测试考上大学的概率; (2)求该学生考上大学的概率.
(2)求该学生考上大学的概率.

解 的不等式
的不等式
选修4—5:不等式选讲
(Ⅰ)若 与2的大小,并说明理由;
与2的大小,并说明理由;
(Ⅱ)设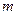 是
是 和1中最大的一个,当
和1中最大的一个,当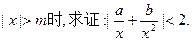
选修4-4:极坐标与参数方程选讲
已知曲线 的极坐标方程为
的极坐标方程为 ,直线
,直线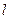 的参数方程是:
的参数方程是:
 .
.
(Ⅰ)求曲线 的直角坐标方程,直线
的直角坐标方程,直线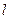 的普通方程;
的普通方程;
(Ⅱ)将曲线 横坐标缩短为原来的
横坐标缩短为原来的 ,再向左平移1个单位,得到曲线曲线
,再向左平移1个单位,得到曲线曲线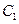 ,求曲线
,求曲线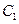 上的点到直线
上的点到直线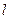 距离的最小值.
距离的最小值.
选修4-1:几何证明选讲
如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧 的中点,连结AG分别交⊙O、BD于点E、F,连结CE.
的中点,连结AG分别交⊙O、BD于点E、F,连结CE.
(Ⅰ)求证: 为⊙O的直径。
为⊙O的直径。
(Ⅱ)求证: ;
;
已知函数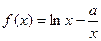 。
。
(Ⅰ)讨论函数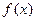 的单调区间;
的单调区间;
(Ⅱ)若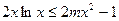 在
在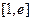 恒成立,求
恒成立,求 的取值范围。
的取值范围。