一般来说,一个人脚掌越长,他的身高就越高.现对10名成年人的脚掌长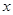 与身高
与身高 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为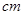 )作为一个样本如上表示.
)作为一个样本如上表示.
| 脚掌长(x) |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
| 身高(y) |
141 |
146 |
154 |
160 |
169 |
176 |
181 |
188 |
197 |
203 |
(1)在上表数据中,以“脚掌长”为横坐标,“身高”为纵坐标,做出散点图后,发现散点在一条直线附近,试求“身高”与“脚掌长”之间的线性回归方程 ;
;
(2)若某人的脚掌长为 ,试估计此人的身高;
,试估计此人的身高;
(3)在样本中,从身高180cm以上的4人中随机抽取2人作进一步的分析,求所抽取的2人中至少有1人身高在190cm以上的概率. (参考数据: ,
, )
)
已知数列{an}中,a1=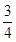 ,an+1=
,an+1= (n∈N*).
(n∈N*).
(1)求证:数列{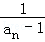 }是等差数列,并求{an}的通项公式;
}是等差数列,并求{an}的通项公式;
(2)设bn+an=l(n∈N*),S=b1b2+b2b3+…+bnbn+1,试比较an与8Sn的大小.
已知向量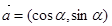 ,
, ,
,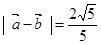 。
。
(1)求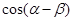 的值;
的值;
(2)若 且
且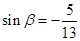 ,求
,求 的值。
的值。
在△ABC中,内角A,B,C的对边分别为a,b,c,若b=1,c= .
.
(Ⅰ)求角C的取值范围;
(Ⅱ)求4sinCcos(C )的最小值.
)的最小值.
已知函数 ,
, .
.
(Ⅰ)若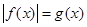 有且仅有两个不同的解,求
有且仅有两个不同的解,求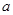 的值;
的值;
(Ⅱ)若当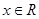 时,不等式
时,不等式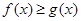 恒成立,求实数
恒成立,求实数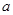 的取值范围;
的取值范围;
(Ⅲ)若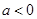 时,求
时,求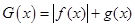 在
在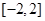 上的最大值.
上的最大值.
已知抛物线 :
: 的准线与
的准线与 轴交于
轴交于 点,
点,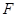 为抛物线
为抛物线 的焦点,过
的焦点,过 点斜率为
点斜率为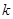 的直线
的直线 与抛物线
与抛物线 交于
交于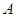 、
、 两点.
两点.
(Ⅰ)若 ,求
,求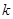 的值;
的值;
(Ⅱ)是否存在这样的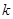 ,使得抛物线
,使得抛物线 上总存在点
上总存在点 满足
满足 ,若存在,求
,若存在,求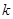 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.