已知点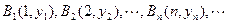 (
(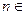 N
N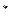 )顺次为直线
)顺次为直线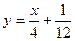 上的点,点
上的点,点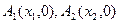
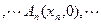 (
(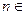 N
N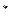 )顺次为
)顺次为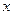 轴上的点,其中
轴上的点,其中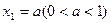 ,对任意的
,对任意的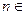 N
N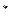 ,点
,点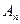 、
、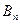 、
、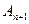 构成以
构成以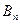 为顶点的等腰三角形.(Ⅰ)证明:数列
为顶点的等腰三角形.(Ⅰ)证明:数列 是等差数列;(Ⅱ)求证:对任意的
是等差数列;(Ⅱ)求证:对任意的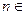 N
N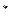 ,
,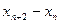 是常数,并求数列
是常数,并求数列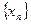 的通项公式; (Ⅲ)在上述等腰三角形
的通项公式; (Ⅲ)在上述等腰三角形 中是否存在直角三角形,若存在,求出此时
中是否存在直角三角形,若存在,求出此时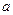 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人面试合格的概率都是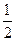 ,且面试是否合格互不影响.求:至少有1人面试合格的概率;
,且面试是否合格互不影响.求:至少有1人面试合格的概率;
某公司是否对某一项目投资,由甲、乙、丙三位决策人投票决定.他们三人都有“同意”、“中立”、“反对”三类票各一张.投票时,每人必须且只能投一张票,每人投三类票中的任何一类票的概率都为 ,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.
,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.
(Ⅰ)求此公司一致决定对该项目投资的概率;
(Ⅱ)求此公司决定对该项目投资的概率;
某人对一目标进行射击,每次命中率都是0.25,若使至少命中1次的概率不小于0.75,至少应射击几次?
假定一批产品共100件,其中有4件不合格品,随机取出的6件产品中,不合格品数X的概率分布如何?
在一个口袋中装有30个球,其中有10个红球,其余为白球,这些球除颜色外完全相同.游戏者一次从中摸出5个球.摸到4个红球就中一等奖,那么获一等奖的概率是多少?