求满足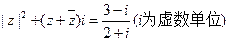 的复数z。
的复数z。
(请考生在题22,23,24中任选一题作答,如果多做,则按所做的第一题计分。)
(本小题满分10分)设函数
(1)求函数 的值域;
的值域;
(2)若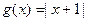 ,求
,求 成立时
成立时 的取值范围。
的取值范围。
(请考生在题22,23,24中任选一题作答,如果多做,则按所做的第一题计分。)
(本小题满分10分)已知圆锥曲线 是参数)和定点
是参数)和定点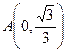 ,F1、F2是圆锥曲线的左、右焦点。
,F1、F2是圆锥曲线的左、右焦点。
(1)求经过点F2且垂直地于直线AF1的直线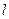 的参数方程;
的参数方程;
(2)以坐标原点为极点,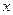 轴的正半轴为极轴建立极坐标系,求直线AF2的极坐标方程。
轴的正半轴为极轴建立极坐标系,求直线AF2的极坐标方程。
(请考生在题22,23,24中任选一题作答,如果多做,则按所做的第一题计分。)
(本小题满分10分)如图5,⊙O1和⊙O2公切线AD和BC相交于点D,A、B、C为切点,直线DO1与⊙O1与E、G两点,直线DO2交⊙O2与F、H两点。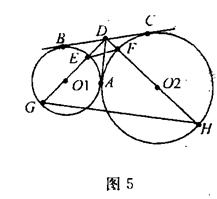
(1)求证: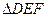 ~
~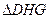 ;
;
(2)若⊙O1和⊙O2的半径之比为9:16,求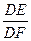 的值。
的值。
(本小题满分12分)已知函数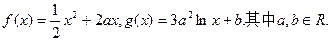
(1)设两曲线 与
与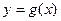 有公共点,且在公共点处的切线相同,若
有公共点,且在公共点处的切线相同,若 ,试建立
,试建立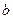 关于
关于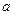 的函数关系式;
的函数关系式;
(2)在(1)的条件下求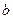 的最大值;
的最大值;
(3 )若
)若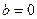 时,函数
时,函数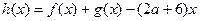 在(0,4)上为单调函数,求
在(0,4)上为单调函数,求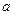 的取值范围。
的取值范围。