(本小题满分13分)随着石油资源的日益紧缺,我国决定建立自己的石油储备基地,
已知某石油储备基地原储有石油 吨,按计划正式运营后的第一年进油量为已储油量的25%,以后每年的进油量均为上一年底储油量的25%,且每年年内用出
吨,按计划正式运营后的第一年进油量为已储油量的25%,以后每年的进油量均为上一年底储油量的25%,且每年年内用出 吨,设
吨,设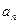 为正式运营后第
为正式运营后第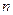 年年底的石油储量.(Ⅰ)求
年年底的石油储量.(Ⅰ)求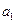 、
、 、
、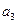 ; (Ⅱ)猜测出
; (Ⅱ)猜测出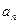 的表达式并用数学归纳法予以证明;(Ⅲ)为抵御突发事件,该油库年底储油量不得少于
的表达式并用数学归纳法予以证明;(Ⅲ)为抵御突发事件,该油库年底储油量不得少于 吨,如果
吨,如果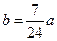 吨,该油库能否长期按计划运营?如果能,请加以证明;如果不能,请说明理由.(计算中可供参考的数据:
吨,该油库能否长期按计划运营?如果能,请加以证明;如果不能,请说明理由.(计算中可供参考的数据: ,
,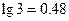 )
)
(本小题满分10分)
已知函数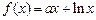
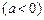 .
.
(I)求 的单调区间;
的单调区间;
(II)设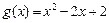 ,若对任意
,若对任意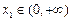 ,均存在
,均存在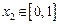 ,使得
,使得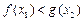 ,求
,求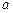 的取值范围.
的取值范围.
(本小题满分10分)
如图,四面体ABCD中,O是BD的中点,ΔABD和ΔBCD均为等边三角形,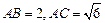 .
.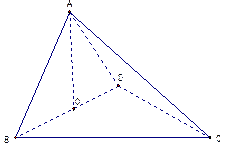
(I)求证: 平面BCD;
平面BCD;
(II)求二面角A-BC- D的正切值.
(本小题满 分10分)
分10分)
如图,在正四棱柱ABCD-A1 B1C1D1中,AA1 =
B1C1D1中,AA1 =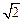 ,AB = 1,E是DD1的中点.
,AB = 1,E是DD1的中点.
(I)求直线B1D和平面A1ADD1所成角的大小;
(II)求证:B1D⊥AE.
(本小题满分10分)
已知复数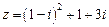 .
.
(I)求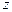 及
及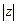 ;
;
(II)若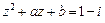 ,求实数
,求实数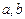 的值.
的值.
(本小题满分16分)
已知函数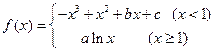 的图象过点
的图象过点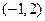 ,且在点
,且在点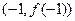 处的切线与直线
处的切线与直线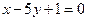 垂直.
垂直.
(1) 求实数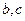 的值;(6分)
的值;(6分)
(2) 求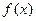 在
在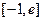 (
(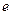 为自然对数的底数)上的最大值;(5分)
为自然对数的底数)上的最大值;(5分)
(3) 对任意给定的正实数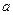 ,曲线
,曲线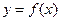 上是否存在两点
上是否存在两点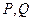 ,使得
,使得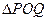 是以
是以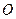 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在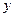 轴上?(5分)
轴上?(5分)