本题(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)(本小题满分7分)选修4-4:坐标系与参数方程
以直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴。已知点
轴的正半轴为极轴。已知点 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点 的极坐标为
的极坐标为 若直线
若直线 过点
过点 ,且倾斜角为
,且倾斜角为 ,圆
,圆 以
以 为圆心、
为圆心、 为半径。
为半径。
(I)求直线 的参数方程和圆
的参数方程和圆 的极坐标方程;
的极坐标方程;
(II)试判定直线 和圆
和圆 的位置关系.
的位置关系.
(2)(本小题满分7分)选修4-4:矩阵与变换
把曲线 先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于
先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于 轴的反射变换变为曲线
轴的反射变换变为曲线 ,求曲线
,求曲线 的方程.
的方程.
(3)(本小题满分7分)选修4-5:不等式选讲
关于 的一元二次方程
的一元二次方程 对任意
对任意 无实根,求实数
无实根,求实数 的取值范围.
的取值范围.
(本小题满分10分)在极坐标中,已知点 为方程
为方程 所表示的曲线上一动点,点
所表示的曲线上一动点,点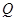 的坐标为
的坐标为 ,求
,求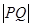 的最小值.
的最小值.
(本小题满分10分)已知矩阵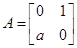 ,矩阵
,矩阵 ,直线
,直线 经矩阵
经矩阵 所对应的变换得到直线
所对应的变换得到直线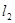 ,直线
,直线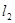 又经矩阵
又经矩阵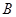 所对应的变换得到直线
所对应的变换得到直线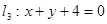 .
.
(1)求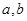 的值;
的值;
(2)求直线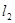 的方程.
的方程.
(本小题满分10分)如图所示,已知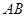 为圆
为圆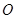 的直径,
的直径,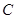 ,
,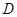 是圆
是圆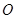 上的两个点,
上的两个点,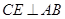 于
于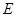 ,
,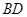 交
交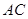 于
于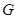 ,交
,交 于
于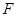 ,
,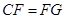 .
.
(1)求证: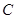 是劣弧
是劣弧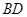 的中点;
的中点;
(2)求证: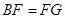 .
.
(本小题满分16分)已知函数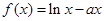 在
在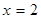 处的切线
处的切线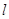 与直线
与直线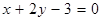 平行.
平行.
(1)求实数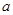 的值;
的值;
(2)若关于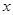 的方程
的方程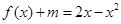 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数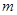 的取值范围;
的取值范围;
(3)记函数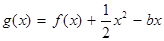 ,设
,设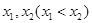 是函数
是函数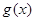 的两个极值点,若
的两个极值点,若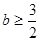 ,且
,且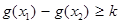 恒成立,求实数
恒成立,求实数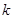 的最大值.
的最大值.
(本小题满分16分)对于给定数列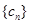 ,如果存在实常数
,如果存在实常数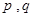 使得
使得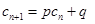 对于任意
对于任意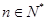 都成立,我们称数列
都成立,我们称数列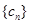 是 “线性数列”.
是 “线性数列”.
(1)若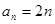 ,
,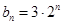 ,
,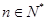 ,数列
,数列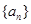 、
、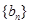 是否为“线性数列”?若是,指出它对应的实常数
是否为“线性数列”?若是,指出它对应的实常数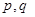 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列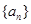 是“线性数列”,则数列
是“线性数列”,则数列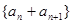 也是“线性数列”;
也是“线性数列”;
(3)若数列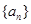 满足
满足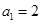 ,
,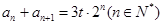 ,
,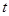 为常数.求数列
为常数.求数列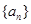 前
前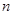 项的和.
项的和.