设向量a =(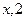 ),b =(
),b =(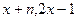 )(
)(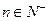 ),函数
),函数 a·b在[0,1]上的最小值与最大值的和为
a·b在[0,1]上的最小值与最大值的和为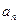 ,又数列{
,又数列{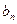 }满足:
}满足: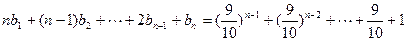 .
.
(1)求证: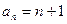 ;
;
(2)求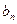 的表达式;
的表达式;
(3)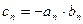 ,试问数列{
,试问数列{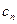 }中,是否存在正整数
}中,是否存在正整数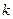 ,使得对于任意的正整数
,使得对于任意的正整数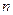 ,都有
,都有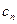 ≤
≤ 成立?证明你的结论.
成立?证明你的结论.
(本小题满分12分)(注意:在试题卷上作答无效)
已知数列 的前
的前 项和
项和 满足
满足 ,数列
,数列 满足
满足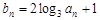 ,其中
,其中 .
. 求数列
求数列 和
和 的通项公式;
的通项公式;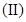 设
设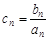 ,数列
,数列 的前
的前 项和为
项和为 ,若
,若 对
对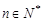 恒成立,求实数
恒成立,求实数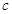 的取值范围.
的取值范围.
(本小题满分12分)(注意:在试题卷上作答无效)
已知定义在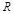 上的函数
上的函数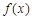 ,对任意
,对任意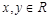 都有
都有 ,且
,且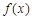 是
是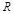 上的增函数.
上的增函数. 求证:函数
求证:函数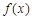 是
是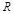 上的奇函数;
上的奇函数;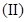 若不等式
若不等式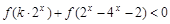 对任意
对任意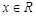 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)(注意:在试题卷上作答无效)
在平面直角坐标系 中,已知直线
中,已知直线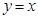 与圆心在第二象限的圆
与圆心在第二象限的圆 相切于原点
相切于原点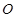 ,且圆
,且圆 与圆
与圆
 的面积相等.
的面积相等. 求圆
求圆 的标准方程;
的标准方程; 试探究圆
试探究圆 上是否存在异于原点的点
上是否存在异于原点的点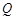 ,使点
,使点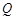 到定点
到定点 的距离等于线段
的距离等于线段 的长?若存在,求出点
的长?若存在,求出点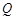 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本小题满分12分)(注意:在试题卷上作答无效)
在平面直角坐标系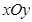 中,已知
中,已知 ,
, .
. 若
若 ∥
∥ ,求
,求 的坐标;
的坐标; 若
若 与
与 垂直,求
垂直,求 与
与 的夹角
的夹角 的大小.
的大小.
(本小题满分12分)(注意:在试题卷上作答无效)
已知函数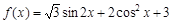 .
. 求
求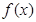 的最小正周期;
的最小正周期; 求
求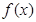 在
在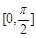 上的最值.
上的最值.