(本小题满分12分)已知△ABC的三个内角分别为A、B、C,向量m = (sinB, 1 – cosB)与向量n= (2,0)夹角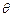 的余弦值为
的余弦值为 . (1)求角B的大小; (2)求sinA + sinC的取值范围.
. (1)求角B的大小; (2)求sinA + sinC的取值范围.
已知椭圆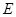 :
: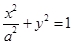 (
(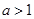 )的离心率
)的离心率 ,直线
,直线 与椭圆
与椭圆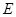 交于不同的两点
交于不同的两点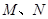 ,以线段
,以线段 为直径作圆
为直径作圆 ,圆心为
,圆心为
(Ⅰ)求椭圆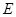 的方程;
的方程;
(Ⅱ)当圆 与
与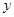 轴相切的时候,求
轴相切的时候,求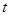 的值;
的值;
(Ⅲ)若 为坐标原点,求
为坐标原点,求 面积的最大值。
面积的最大值。
已知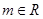 ,命题
,命题 :对任意
:对任意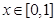 ,不等式
,不等式 恒成立;命题
恒成立;命题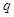 :存在
:存在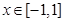 ,使得
,使得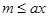 成立
成立
(Ⅰ)若 为真命题,求
为真命题,求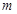 的取值范围;
的取值范围;
(Ⅱ)当 ,若
,若 且
且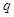 为假,
为假, 或
或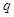 为真,求
为真,求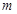 的取值范围。
的取值范围。
(Ⅲ)若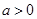 且
且 是
是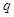 的充分不必要条件,求
的充分不必要条件,求 的取值范围。
的取值范围。
从一副扑克牌的红桃花色中取5张牌,点数分别为1、2、3、4、5,甲、乙两人玩一种游戏:
甲先取一张牌,记下点数,放回后乙再取一张牌,记下点数.如果两个点数的和为偶数就算甲胜,否则算乙胜.
(Ⅰ)求甲胜且点数的和为6的事件发生的概率;
(Ⅱ)分别求出甲胜与乙胜的概率,判断这种游戏规则公平吗?
我市为积极相应《全民健身条例》大力开展学生体育活动,如图是委托调查机构在市区的两所学校A校、B校中分别随机抽取了10名高二年级的学生当月体育锻炼时间的茎叶图(单位:小时)
(Ⅰ)根据茎叶图,分别写将两所学校学生当月体育锻炼时间的众数、中位数和平均数填入下表;
(Ⅱ)根据茎叶图,求A校学生的月体育锻炼时间的方差;
(Ⅲ)若学生月体育锻炼的时间低于10小时,就说明该生体育锻炼时间严重不足。根据茎叶图估计 两所学校的学生体育锻炼严重不足的频率。
两所学校的学生体育锻炼严重不足的频率。
设复数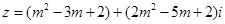
 ,
,
(Ⅰ)若 是实数,求
是实数,求 的值;
的值;
(Ⅱ)若 对应的点位于复平面第四象限,求
对应的点位于复平面第四象限,求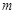 的取值范围.
的取值范围.