(本小题满分12分)
设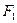 、
、 分别是椭圆
分别是椭圆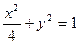 的左、右焦点.
的左、右焦点.
(1)若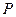 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求
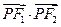 的取值范围;
的取值范围;
(2)设过定点Q(0,2)的直线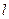 与椭圆交于不同的两点M、N,且∠
与椭圆交于不同的两点M、N,且∠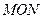 为锐角(其中
为锐角(其中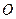 为坐标原点),求直线
为坐标原点),求直线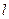 的斜率
的斜率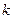 的取值范围.
的取值范围.
(3)设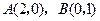 是它的两个顶点,直线
是它的两个顶点,直线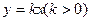 与AB相交于点D,与椭圆相交于E、F两点.求四边形
与AB相交于点D,与椭圆相交于E、F两点.求四边形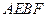 面积的最大值.
面积的最大值.
在某次竞赛活动中(竞赛以笔试形式进行),文科班有2名同学参加数学竞赛,另有2名同学参加英语竞赛;理科班有2名同学参加数学竞赛,另有3名同学参加英语竞赛。后由于某种原因,参加数学和英语竞赛的同学各有一名同学交换考试。
(1)求参加数学竞赛恰有2名文科同学的概率。
(2)求参加数学竞赛的文科同学数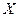 的分布列。
的分布列。
已知等式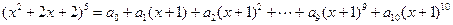 ,其中
,其中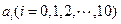 为实常数,求
为实常数,求
(1) 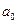 (2)
(2) 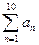 (3)
(3)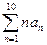
某医院有内科医生12名,外科医生8名,现要派5名医生参加赈灾医疗队,其中,
(1)内科医生甲必须参加,外科医生乙因故不能参加,有多少种选法。
(2)内科医生和外科医生都要有人参加,有多少种选法。
已知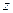 是复数,
是复数,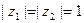 ,
,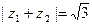 ,求
,求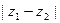

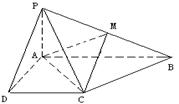
已知四棱锥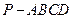 的底面为直角梯形,
的底面为直角梯形,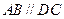 ,
,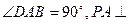 底面
底面 ,且
,且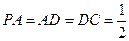 ,
,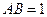 ,
,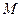 是
是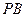 的中点。
的中点。
(Ⅰ)证明:面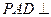 面
面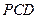 ;
;
(Ⅱ)求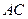 与
与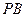 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求面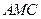 与面
与面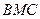 所成二面角的余弦值.
所成二面角的余弦值.