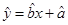在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证PC⊥平面AEF;
(Ⅲ)求证CE∥平面PAB.
如图,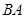 是圆
是圆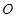 的直径,
的直径,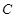 、
、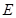 在圆
在圆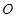 上,
上, 、
、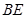 的延长线交直线
的延长线交直线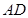 于点
于点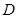 、
、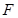 ,
,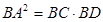 求证:
求证:
(Ⅰ)直线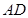 是圆
是圆 的切线;
的切线;
(Ⅱ)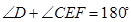

设函数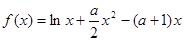 (
(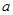 为常数)
为常数)
(Ⅰ)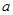 =2时,求
=2时,求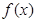 的单调区间;
的单调区间;
(Ⅱ)当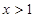 时,
时,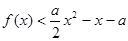 ,求
,求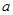 的取值范围
的取值范围
已知椭圆 的右焦点为
的右焦点为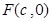 ,上顶点为B,离心率为
,上顶点为B,离心率为 ,圆
,圆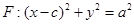 与
与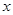 轴交于
轴交于 两点
两点
(Ⅰ)求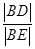 的值;
的值;
(Ⅱ)若 ,过点
,过点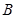 与圆
与圆 相切的直线
相切的直线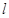 与
与 的另一交点为
的另一交点为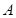 ,求
,求 的面积
的面积
如图,四边形 是正方形,
是正方形, ,
,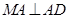 ,
,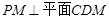 ,
, 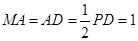
(Ⅰ)求证:平面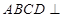 平面
平面 ;
;
(Ⅱ)求三棱锥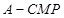 的高
的高 
下表是某单位在2013年1—5月份用水量(单位:百吨)的一组数据:
月份 |
1 |
2 |
3 |
4 |
5 |
用水量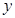 |
4 5 |
4 |
3 |
2 5 |
1 8 |
(Ⅰ)若由线性回归方程得到的预测数据与实际检验数据的误差不超过0 05,视为“预测可靠”,通过公式得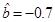 ,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;
,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;
(Ⅱ)从这5个月中任取2个月的用水量,求所取2个月的用水量之和小于7(单位:百吨)的概率
参考公式:回归直线方程是: ,
,