已知数列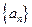 是首项
是首项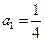 的等比数列,其前
的等比数列,其前 项和
项和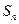 中
中 ,
,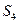 ,
,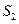 成等差数列,
成等差数列,
(1)求数列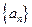 的通项公式;
的通项公式;
(2)设 ,若
,若 ≤
≤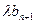 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
已知:sinα=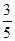 ,cos(α+β)=-
,cos(α+β)=-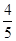 ,0<α<
,0<α<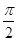 ,π<α+β<
,π<α+β<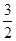 π,求cosβ的值.
π,求cosβ的值.
某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
①列出所有可能的抽取结果;
②求抽取的2所学校均为小学的概率.
已知f(x)=sinx+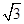 cosx(x∈R).
cosx(x∈R).
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的最大值,并指出此时x的值.
对甲、乙的学习成绩进行抽样分析,各抽5门功课,得到的观测值如下:
通过计算,回答:甲、乙谁的平均成绩较好?谁的各门功课发展较平衡?
设数列{an}共有n( )项,且
)项,且 ,对每个i (1≤i≤
,对每个i (1≤i≤ ,i
,i N),均有
N),均有 .
.
(1)当 时,写出满足条件的所有数列{an}(不必写出过程);
时,写出满足条件的所有数列{an}(不必写出过程);
(2)当 时,求满足条件的数列{an}的个数.
时,求满足条件的数列{an}的个数.