下图是某市有关部门根据对某地干部的月收入情况调查后画出的样本频率分布直方图,已知图中第一组的频数为4000.请根据该图提供的信息解答下列问题:(图中每组包括左端点,不包括右端点,如第一组表示收入在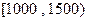 )
)
(1)求样本中月收入在 的人数;
的人数;
(2)为了分析干部的收入与年龄、职业等方面的关系,必须从样本的各组中按月收入再用分层抽样方法抽出 人作进一步分析,则月收入在
人作进一步分析,则月收入在 的这段应抽多少人?
的这段应抽多少人?
(3)试估计样本数据的中位数.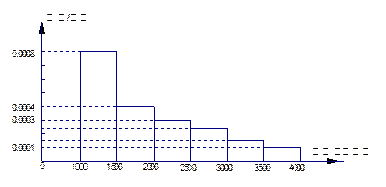
已知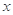 ,
,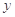 满足约束条件
满足约束条件 求
求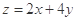 的最小值与最大值。
的最小值与最大值。
已知等差数列{an}的前n项的和记为Sn.如果a4=-12,a8=-4.
(1)求数列{an}的通项公式;(2)求Sn的最小值及其相应的n的值;
(3)从数列{an}中依次取出a1,a2,a4,a8,…, ,…,构成一个新的数列{bn},
,…,构成一个新的数列{bn},
求{bn}的前n项和
已知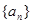 是等差数列,其前n项和为Sn,已知
是等差数列,其前n项和为Sn,已知
(1)求数列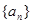 的通项公式;
的通项公式;
(2)设 ,证明
,证明 是等比数列,并求其前n项和Tn.
是等比数列,并求其前n项和Tn.
在 中,
中,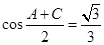 .
.
(1)求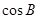 的值;(2)若
的值;(2)若 ,
, ,求
,求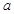 和
和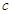 的值。
的值。
某同学利用暑假时间到一家商场勤工俭学,该商场向他提供了三种付款方式:第一种,每天支付38圆;第二种,第一天付4元,第二天付8元,第三天付12元,以此类推:第三种,第一天付0.4元,以后每天比前一天翻一番(即增加一倍),
你会选择哪种方式领取报酬呢?