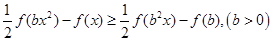在等差数列 中,
中, ,
, .令
.令 ,数列
,数列 的前
的前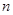 项和为
项和为 .
.
(1)求数列 的通项公式和
的通项公式和 ;
;
(2)是否存在正整数 ,
,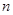 (
(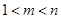 ),使得
),使得 ,
,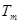 ,
, 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有
的 ,
,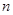 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
求经过三点A(1,-1),B(1,4),C(4,-2)的圆的方程,并判断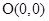 与圆的位置关系。
与圆的位置关系。
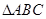 的三外顶点分别为
的三外顶点分别为 .
.
(1)求边AC所在的直线方程;
(2)求AC边上的中线BD所在的直线的方程。
求倾斜角是45°,并且与原点的距离是5的直线的方程.
(14分)已知函数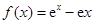 .
.
(Ⅰ)求函数 的最小值;
的最小值;
(Ⅱ)求证:
 ;
;
(Ⅲ)对于函数 与
与 定义域上的任意实数
定义域上的任意实数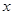 ,若存在常数
,若存在常数 ,使得
,使得 和
和 都成立,则称直线
都成立,则称直线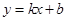 为函数
为函数 与
与 的“分界线”.设函数
的“分界线”.设函数 ,
, ,
, 与
与 是否存在“分界线”?若存在,求出
是否存在“分界线”?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
设函数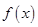 对任意
对任意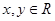 ,都有
,都有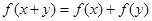 ,当
,当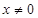 时,
时,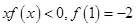
(1)求证: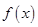 是奇函数;
是奇函数;
(2)试问:在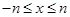 时
时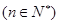 ,
,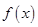 是否有最大值?如果有,求出最大值,如果没有,说明理由.
是否有最大值?如果有,求出最大值,如果没有,说明理由.
(3)解关于x的不等式