已知抛物线C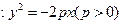
上横坐标为
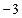的一点，与其焦点的距离为4.（1）求
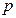的值；（2）设动直线
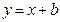与抛物线C相交于A.B两点，问在直线
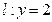上是否存在与
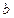的取值无关的定点M，使得
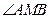被直线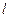
平分？若存在，求出点M的坐标；若不存在，说明理由.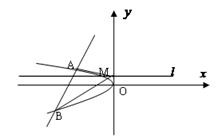
已知数列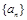
满足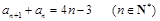
.
（1）若数列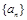是等差数列，求其公差
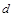的值;
（2）若数列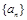的首项
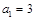，求数列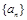的前100项的和.
某厂生产某种产品的年固定成本为250万元，每生产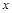
万件，需另投入的成本为
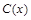（单位：万元），当年产量小于80万件时，
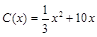;当年产量不小于80万件时，
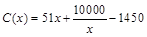.假设每万件该产品的售价为50万元，且该厂当年生产的该产品能全部销售完.
（1）写出年利润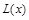
（万元）关于年产量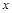（万件）的函数关系式；
（2）年产量为多少万件时，该厂在该产品的生产中所获利润最大？最大利润是多少？
已知函数
，若直线
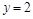是函数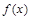
图象的一条切线.
（1）求函数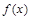的解析式；
（2）若函数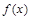图象上的两点
、
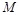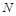的横坐标依次为2和4，
为坐标原点，求△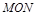
的面积.
已知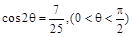
.
（1）求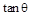
的值；
（2）求
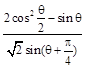的值.
已知集合
集合
.
（1）若
,求
;
（2）若
,求实数
的取值范围.