如图,四边形ABCD为矩形,平面ABCD⊥平面ABE,
BE=BC,F为CE上的一点,且BF⊥平面ACE.
(1)求证:AE⊥BE;
(2)求证:AE∥平面BFD.
设函数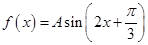 (
(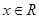 )的图象过点
)的图象过点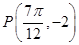 .
.
(Ⅰ)求 的解析式;(Ⅱ)已知
的解析式;(Ⅱ)已知 ,
,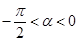 ,求
,求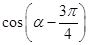 的值.
的值.
在直角坐标系xOy中,曲线C1的点均在C2:(x-5)2+y2=9外,且对C1上任意一点M,M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值.
(Ⅰ)求曲线C1的方程;
(1-4班做)(Ⅱ)设P(x0,y0)(y0≠±3)为圆C2外一点,过P作圆C2的两条切线,分别与曲线C1相交于点A,B和C,D.证明:当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值.
(5-7班做)(Ⅱ)设P(-4,1)为圆C2外一点,过P作圆C2的两条切线,分别与曲线C1相交于点A,B和C,D.证明:四点A,B,C,D的纵坐标之积为定值.
如图,已知三棱柱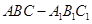 的侧棱与底面垂直,
的侧棱与底面垂直, ,
,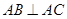 ,
,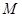 ,
,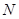 分别是
分别是 ,
, 的中点,点
的中点,点 在直线
在直线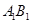 上,且
上,且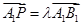 ;
;
(Ⅰ)证明:无论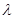 取何值,总有
取何值,总有 ;
;
(Ⅱ)当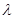 取何值时,直线
取何值时,直线 与平面
与平面 所成的角
所成的角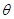 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;
(Ⅲ)是否存在点 ,使得平面
,使得平面 与平面
与平面 所成的二面角为30º,若存在,试确定点
所成的二面角为30º,若存在,试确定点 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
已知圆C: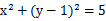 ,直线L:
,直线L:
(1)求证:对m ,直线L与圆C总有两个交点;
,直线L与圆C总有两个交点;
(2)设直线L与圆C交于点A、B,若|AB|= ,求直线L的倾斜角;
,求直线L的倾斜角;
(3)设直线L与圆C交于A、B,若定点P(1,1)满足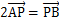 ,求此时直线L的方程.
,求此时直线L的方程.
如图,在直三棱柱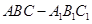 中,
中, 、
、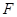 分别是
分别是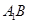 、
、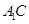 的中点,点
的中点,点 在
在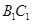 上,
上,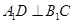 。
。 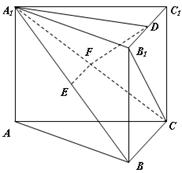
求证:(1)EF∥平面ABC;
(2)平面
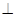 平面
平面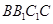 .
.