如右图(1)所示,定义在区间 上的函数
上的函数 ,如果满
,如果满
足:对 ,
, 常数A,都有
常数A,都有 成立,则称函数
成立,则称函数  在区间
在区间 上有下界,其中
上有下界,其中 称为函数的下界. (提示:图(1)、(2)中的常数
称为函数的下界. (提示:图(1)、(2)中的常数 、
、 可以是正数,也可以是负数或零)
可以是正数,也可以是负数或零) (Ⅰ)试判断函数
(Ⅰ)试判断函数 在
在 上是否有下界?并说明理由;
上是否有下界?并说明理由;
(Ⅱ)又如具有右图(2)特征的函数称为在区间 上有上界.
上有上界.
请你类比函数有下界的定义,给出函数 在区间
在区间 上
上
有上界的定义,并判断(Ⅰ)中的函数在 上是否
上是否
有上界?并说明理由;
(Ⅲ)若函数 在区间
在区间 上既有上界又有下界,则称函数
上既有上界又有下界,则称函数 在区间
在区间 上有界,函数
上有界,函数 叫做有界函数.试探究函数
叫做有界函数.试探究函数 (
(

 是常数)是否是
是常数)是否是 (
(
 、
、 是常数)上的有界函数?
是常数)上的有界函数?
已知函数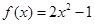 .
.
(1)用定义证明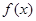 是偶函数;
是偶函数;
(2)用定义证明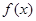 在
在 上是减函数;
上是减函数;
(3)作出函数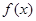 的图像,并写出函数
的图像,并写出函数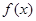 当
当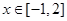 时的最大值与最小值.
时的最大值与最小值.
已知集合A=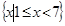 ,B={x|2<x<10},C={x|x<a},全集为实数集R.
,B={x|2<x<10},C={x|x<a},全集为实数集R.
(1)求A∪B, ; (2)如果A∩C≠φ,求a的取值范围.
; (2)如果A∩C≠φ,求a的取值范围.
计算:
(1)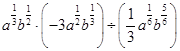 ,
,
(2)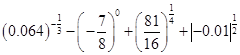
(本小题满分14分)定义在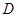 上的函数
上的函数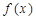 ,如果满足:对任意
,如果满足:对任意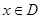 ,存在常数
,存在常数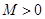 ,都有
,都有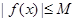 成立,则称
成立,则称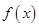 是
是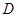 上的有界函数,其中
上的有界函数,其中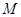 称为函数
称为函数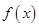 的上界.
的上界.
已知函数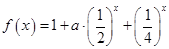 ;
;
(1)当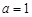 时,求函数
时,求函数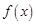 在
在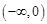 上的值域,并判断函数
上的值域,并判断函数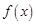 在
在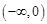 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数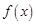 在
在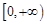 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数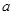 的取值范围
的取值范围
(本小题满分14分)已知函数f(x)=ax+ (a>1).
(a>1).
(1)判定函数f(x)在(-1,+∞)上的单调性,并给出证明;
(2)证明方程f(x)=0没有负数根.