高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
(1)根据上面图表,①②③④处的数值分别为多少?
(2)根据题中信息估计总体平均数是多少?
(3)估计总体落在[129,150]中的概率.
| 分组 |
频数 |
频率 |
 |
① |
② |
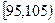 |
|
0.050 |
 |
|
0.200 |
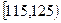 |
12 |
0.300 |
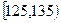 |
|
0.275 |
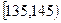 |
4 |
③ |
| [145,155] |
|
0.050 |
| 合计 |
④ |
|
定义在R上的单调函数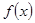 满足
满足 且对任意
且对任意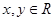 都有
都有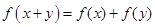 .
.
(1)求证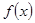 为奇函数;
为奇函数;
(2)若 对任意
对任意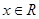 恒成立,求实数
恒成立,求实数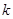 的取值范围.
的取值范围.
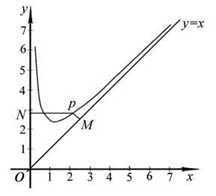
设函数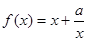 定义域为
定义域为 ,且
,且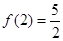 .设点
.设点 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点 分别作直线
分别作直线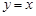 和
和 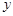 轴的垂线,垂足分别为
轴的垂线,垂足分别为 .
.
(1)写出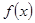 的单调递减区间(不必证明);
的单调递减区间(不必证明);
(2)问: 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;
(3)设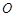 为坐标原点,求四边形
为坐标原点,求四边形 面积的最小值.
面积的最小值.
设函数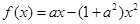 ,其中
,其中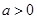 ,区间
,区间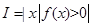
(Ⅰ)求的长度(注:区间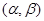 的长度定义为
的长度定义为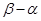 );
);
(Ⅱ)给定常数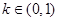 ,当时,求长度的最小值.
,当时,求长度的最小值.
已知函数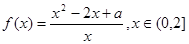 ,其中常数a > 0.
,其中常数a > 0.
(1) 当a = 4时,证明函数f(x)在 上是减函数;
上是减函数;
(2) 求函数f(x)的最小值.
已知函数 .
.
(1)求函数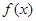 的定义域
的定义域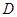 ,并判断
,并判断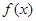 的奇偶性;
的奇偶性;
(2)用定义证明函数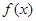 在
在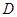 上是增函数;
上是增函数;
(3)如果当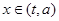 时,函数
时,函数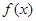 的值域是
的值域是 ,求
,求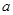 与
与 的值.
的值.