(本小题满分18分)过直线 上的点
上的点 作椭圆
作椭圆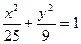 的切线
的切线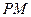 、
、 ,切点分别为
,切点分别为 、
、 ,联结
,联结 (1)当点
(1)当点 在直线
在直线 上运动时,证明:直线
上运动时,证明:直线 恒过定点
恒过定点 ;
;
(2)当 ∥
∥ 时,定点
时,定点 平分线段
平分线段
(本题9分)给出下面的数表序列:
| 表1 |
表2 |
表3 |
… |
| 1 |
1 3 |
1 3 5 |
|
| 4 |
4 8 |
||
| 12 |
其中表 有
有 行,第1行的
行,第1行的 个数
个数 是1,3,5,…,
是1,3,5,…, ,从第2行起,每行中的每个数都等于它肩上的两数之和。
,从第2行起,每行中的每个数都等于它肩上的两数之和。
(1)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表 (不要求证明)
(不要求证明)
(2)每个数表中最后一行都只有一个数,它们构成数列1,4,12,…,记此数列为 ,求数列
,求数列 的前
的前 项和
项和
(本小题满分14分)
将数列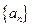 中的所有项按每一行比上一行多一项的规则排成如下数表
中的所有项按每一行比上一行多一项的规则排成如下数表 :
: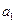
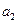
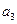
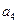
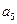
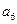
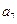
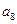
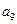
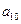
………………………
记表中的第一列数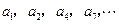 构成的数列为
构成的数列为 ,
, .
.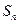 为数列
为数列 的前
的前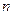 项和,且满足
项和,且满足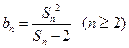 .
.
(1)证明: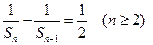 ;
;
(2)求数列 的通项公式;
的通项公式;
(3)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当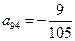 时,求上表中第
时,求上表中第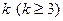 行所有项的和.
行所有项的和.
(本小题满分14分)
已知向量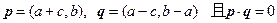 ,其中角
,其中角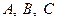 是
是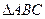 的内角,
的内角, 分别是角
分别是角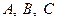 的对边.
的对边.
(1)求角C的大小;
(2)求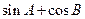 的取值范围.
的取值范围.
(本小题满分14分)
已知二次函数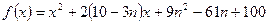 ,其中
,其中 .
.
(1)设函数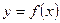 的图象的顶点的横坐标
的图象的顶点的横坐标 构成数列
构成数列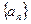 ,求证:数列
,求证:数列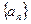 为等差数
为等差数 列;
列;
(2)设函数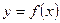 的图象的顶点到
的图象的顶点到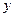 轴的距离构成数列
轴的距离构成数列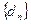 ,求数列
,求数列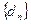 的前
的前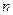 项和
项和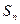 .
.
(本小题满分14分)
某工厂生产A、B型两类产品,每个产品需粗加工和精加工两道工序完成. 已知粗加工做一个A、B型产品分别需要1小时和2小时,精加工一个A、B型产品分别需要3小时和1小时;又知粗加工、精加工每天工作分别不得超过8小时和9小时,而工厂生产一个A、B型产品分别获利润200元和300元,试问工厂每天应生产A、B型产品各多少个,才能获得利润最大?