能否将下列数组中的数填入3×3的方格表,每个小方格中填一个数,使得每行、每列、两条对角线上的3个数的乘积都相等?若能,请给出一种填法;若不能,请给予证明.(Ⅰ)2,4,6,8,12,18,24,36,48; (Ⅱ)2,4,6,8,12,18,24,36,72.
已知A、B、C是平面上任意三点,BC=a,CA=b,AB=c,求y= +
+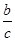 的最小值.
的最小值.
为保增长、促发展,某地计划投资甲、乙两个项目,根据市场调研,知甲项目每投资100万元需要配套电能2万千瓦时,可提供就业岗位24个,GDP增长260万元;乙项目每投资100万元需要配套电能4万千瓦时,可提供就业岗位36个,GDP增长200万元.已知该地为甲、乙两个项目最多可投资3000万元,配套电能100万千瓦时,若要求两个项目能提供的就业岗位不少于840个,问如何安排甲、乙两个项目的投资额,才能使GDP增长的最多.
已知x,y满足约束条件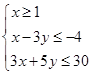
(1)求目标函数z=2x-y的最大值和最小值;
(2)若目标函数z=ax+y取得最大值的最优解有无穷多个,求a的值;
(3)求z=x2+y2的取值范围.
已知α,β是三次函数f(x)=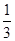 x3+
x3+ ax2+2bx(a,b∈R)的两个极值点,且α∈(0,1),β∈(1,2),求动点(a,b)所在的区域面积S.
ax2+2bx(a,b∈R)的两个极值点,且α∈(0,1),β∈(1,2),求动点(a,b)所在的区域面积S.
已知实数x,y满足不等式组 ,若目标函数z=y-ax取得最大值时的唯一最优解是(1,3),求实数a的取值范围.
,若目标函数z=y-ax取得最大值时的唯一最优解是(1,3),求实数a的取值范围.