如图,甲船以每小时 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于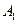 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西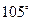 方向的
方向的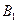 处,此时两船相距
处,此时两船相距 海里,当甲船航行
海里,当甲船航行 分钟到达
分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的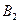 处,此时两船相距
处,此时两船相距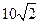 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?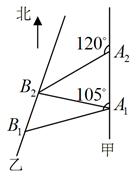
(本小题满分12分)如图是函数f(x)=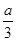 x3-2x2+3a2x的导函数y=
x3-2x2+3a2x的导函数y=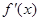 的简图,它与x轴的交点是(1,0)和(3,0)
的简图,它与x轴的交点是(1,0)和(3,0)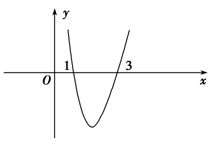
(1)求函数f(x)的极小值点和单调递减区间;
(2)求实数a的值.
(本小题满分12分)已知集合U=R,集合A={x|(x-2)(x-3)<0},函数y=lg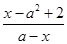 的定义域为集合B.
的定义域为集合B.
(1)若a= ,求集合A∩(∁UB);
,求集合A∩(∁UB);
(2)命题p:x∈A,命题q:x∈B,若q是p的必要条件,求实数a的取值范围.
(本小题满分10分)已知函数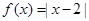 ,
, ,
,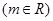 .
.
(1)解关于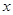 的不等式
的不等式 ;
;
(2)若不等式 对任意
对任意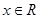 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分12分)已知函数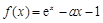 (
(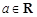 ).
).
(1)求函数 的单调区间;
的单调区间;
(2)函数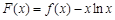 在定义域内存在零点, 求
在定义域内存在零点, 求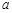 的取值范围.
的取值范围.
(3)若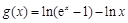 ,当
,当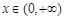 时,不等式
时,不等式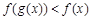 恒成立,求
恒成立,求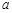 的取值范围.
的取值范围.
(本小题满分12分)已知关于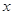 的函数
的函数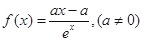
(1)当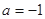 时,求函数
时,求函数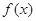 的极值;
的极值;
(2)若函数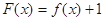 没有零点,求实数
没有零点,求实数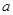 的取值范围.
的取值范围.