设
，
．证明：当且仅当
时，存在数列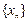
满足以下条件：
（ⅰ）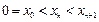
，
；
（ⅱ）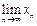
存在；
（ⅲ）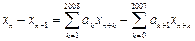
，．
设集合
，
.
（1）当
1时，求集合
；
（2）当
时，求
的取值范围．
已知函数
，其中角
的终边经过点
，且
.
（1）求的值；
（2）求
在
上的单调减区间．
如图已知椭圆的中点在原点，焦点在x轴上，长轴是短轴的2倍且过点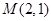
，平行于
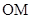的直线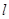
在y轴的截距为
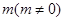，且交椭圆与
两点，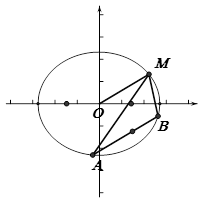
（1）求椭圆的方程；（2）求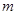
的取值范围；（3）求证：直线
、
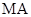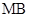与x轴围成一个等腰三角形，说明理由.
设双曲线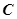
以椭圆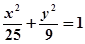
的两个焦点为焦点,且双曲线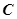的一条渐近线是
，
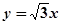(1)求双曲线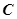的方程；
(2)若直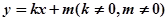线
与双曲线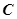交于不同两点
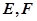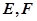,且都在以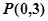
为圆心的圆上,求实数
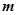的取值范围.
有一个不透明的袋子，装有4个完全相同的小球，球上分别编有数字1，2，3，4，
（1）若逐个不放回取球两次，求第一次取到球的编号为偶数且两个球的编号之和能被3整除的概率；
（2）若先从袋中随机取一个球，该球的编号为a，将球放回袋中，然后再从袋中随机取一个球，该球的编号为b，求直线ax+by+1=0与圆
有公共点的概率.