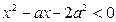已知数列 的前
的前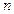 项和
项和 满足
满足
(1)证明 是等比数列.
是等比数列.
(2)设 ,求证:
,求证: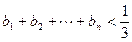
降雨量是指水平地面单位面积上所降水的深度,现用上口直径为32cm,底面直径为24cm、深度为35cm的圆台形水桶来测量降雨量,如果在一次降雨过程中,此桶中的雨水深度为桶深的四分之一,求此次降雨量为多少?(圆台的体积公式为 )
)
如图:在四棱台ABCD-A1B1C1D1中,DD1垂直底面,且DD1=2,底面四边形ABCD与A1B1C1D1分别为边长2和1的正方形.
(1)求直线DB1与BC1夹角的余弦值;
(2)求二面角A-BB1-C的余弦值.
如图,空间四边形OABC各边以及AC,BO的边长都为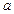 ,点D,E分别是边OA,BC的中点,连结DE
,点D,E分别是边OA,BC的中点,连结DE
(1)计算DE的长; (2)求A点到平面OBC的距离.
本题满分10分)解关于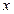 的不等式
的不等式