学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为 ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以 轴为对称轴、
轴为对称轴、 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为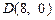 . 观测点
. 观测点 同时跟踪航天器.求航天器变轨后的运行轨迹所在的曲线方程。
同时跟踪航天器.求航天器变轨后的运行轨迹所在的曲线方程。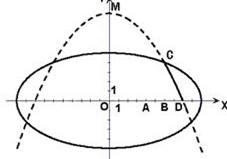
(本小题满分14分)
如图,已知椭圆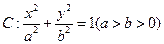 的离心率为
的离心率为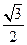 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为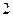 .设直线
.设直线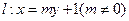 与椭圆
与椭圆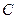 相交于
相交于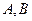 两点,点
两点,点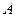 关于
关于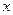 轴对称点为
轴对称点为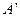 .
.
(1)求椭圆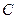 的方程;
的方程;
(2)若以线段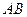 为直径的圆过坐标原点
为直径的圆过坐标原点
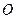 ,求直线
,求直线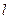 的方程;
的方程;
(3)试问:当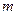 变化时,直线
变化时,直线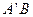 与
与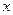 轴是否交于一个定点?若是,请写出定点的坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一个定点?若是,请写出定点的坐标,并证明你的结论;若不是,请说明理由.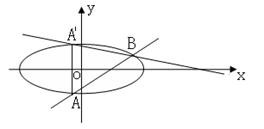
(本小题满分12分)
已知数列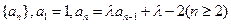 .
.
(1)当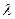 为何值时,数列
为何值时,数列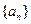 可以构成公差不为零的等差数列,并求其通项公式;
可以构成公差不为零的等差数列,并求其通项公式;
(2)若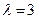 ,令
,令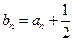 ,求数列
,求数列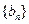 的前
的前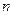 项和
项和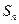 .
.
(本小题满分12分)
已知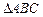 是边长为2的等边三角形,
是边长为2的等边三角形,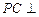 平面
平面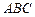 ,
,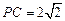 ,
,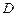 是
是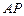 上一动点.
上一动点.
(1)若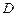 是
是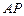 的中点,求直线
的中点,求直线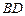 与平面
与平面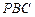 所成的角的正弦值;
所成的角的正弦值;
(2)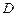 在运动过程中,是否有可能使
在运动过程中,是否有可能使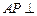 平面
平面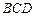 ?请说明理
?请说明理 由.
由.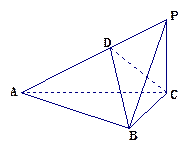
(本小题满分12分)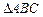 的两个顶点坐标分别是
的两个顶点坐标分别是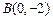 和
和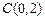 ,顶点A满足
,顶点A满足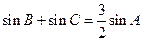 .
.
(1)求顶点A的轨迹方程;
(2)若点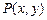 在(1)轨迹上,求
在(1)轨迹上,求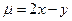 的最值.
的最值.
(本小题满分12分)
设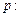 实数
实数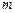 满足
满足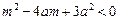 (其中
(其中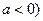 ;
;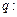 实数
实数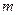 满足方程
满足方程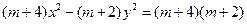 为双曲线.若
为双曲线.若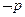 是
是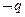 的必要不充分条件,求实数
的必要不充分条件,求实数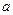 的取值范围.
的取值范围.