双曲线中心在原点,坐标轴为对称轴,与圆x2+y2=17交于A(4,-1).若圆在点A的切线与双曲线的一条渐近线平行,求双曲线的方程.
甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一昼夜内到达该码头的时刻是等可能的,如果甲船停泊时间为1h,乙船停泊时间为2h,求它们中的任意一艘都不需要等待码头空出的概率.
利用随机模拟的方法近似计算图3312中阴影部分(y=2-2x-x2与x轴围成的图形)的面积.
图3-3-12
利用随机模拟法求如图3-3-11所示正方形内随机地投掷飞镖,求飞镖落在阴影部分的概率.
图3-3-11
一个小组有6个同学,选1个为小组长,用随机模拟法估计甲被选的概率,下面步骤错误的是( )
①把六名同学编号1~6②利用计算器的RANDI(1,6)或计算机的RANDBETWEEN(1,6)产生1到6之间整数值的随机数③统计总试验次数N及甲的编号出现的个数N1 ④计算频率fn(A)= 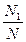 ,即为甲被选的概率的近似值 ⑤
,即为甲被选的概率的近似值 ⑤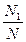 一定等于
一定等于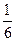
A.②④B.①③④C.⑤D.①④
在墙上挂着一块边长为16cm的正方形木板,上面画了大、中、小三个同心圆,半径分别为2cm、4cm、6cm,某人站在3m之外向此板投镖,设投中线上或没有投中木板时不算,可重投,问:
(1)投中大圆内的概率是多少?
(2)投中小圆与中圆形成的圆环的概率是多少?
(3)投中大圆之外的概率是多少?