设0≤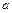 ≤
≤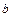 ≤
≤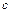 ≤1,求证:
≤1,求证: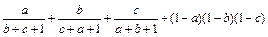 ≤1
≤1
已知抛物线 与圆
与圆 的两个交点之间的距离为4.
的两个交点之间的距离为4.
(1)求 的值;
的值;
(2)设过抛物线 的焦点
的焦点 且斜率为
且斜率为 的直线与抛物线交于
的直线与抛物线交于 两点,与圆
两点,与圆 交于
交于 两点,当
两点,当 时,求
时,求 的取值范围.
的取值范围.
如图,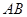 是圆
是圆 的直径,
的直径, 是圆
是圆 上异于
上异于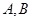 的一个动点,
的一个动点,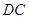 垂直于圆
垂直于圆 所在的平面,
所在的平面,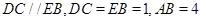 .
.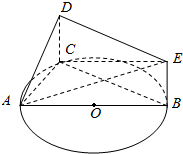
(1)求证: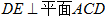 ;
;
(2)若 ,求平面
,求平面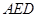 与平面
与平面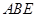 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
某校校庆,各届校友纷至沓来,某班共来了 位校友(
位校友( ),其中女校友6位,组委会对这
),其中女校友6位,组委会对这 位校友登记制作了一份校友名单,现随机从中选出2位校友代表,若选出的2位校友是一男一女,则称为“最佳组合” ..
位校友登记制作了一份校友名单,现随机从中选出2位校友代表,若选出的2位校友是一男一女,则称为“最佳组合” ..
(1)若随机选出的2位校友代表为“最佳组合”的概率不小于 ,求
,求 的最大值;
的最大值;
(2)当 时,设选出的2 位校友代表中女校友人数为
时,设选出的2 位校友代表中女校友人数为 ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.
已知数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
选修4-5:不等式选讲
已知函数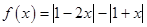
(1)解不等式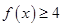 ;
;
(2)若函数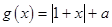 的图象恒在函数
的图象恒在函数 的图象的上方,求实数
的图象的上方,求实数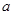 的取值范围.
的取值范围.