(本小题满分12分)
求经过点 ,且满足下列条件的直线方程:
,且满足下列条件的直线方程:
(1)倾斜角的正弦为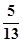 ; (2)与两坐标轴的正半轴围成的三角形面积为4。
; (2)与两坐标轴的正半轴围成的三角形面积为4。
(本小题满分12分)已知函数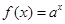 的图象过点
的图象过点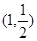 ,且点
,且点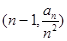
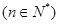 在函数
在函数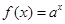 的图象上.
的图象上.
(1)求数列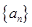 的通项公式;
的通项公式;
(2)令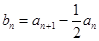 ,若数列
,若数列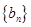 的前
的前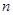 项和为
项和为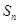 ,求证:
,求证: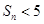 .
.
(本小题满分12分)在平面直角坐标系中,点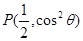 在角
在角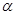 的终边上,点
的终边上,点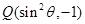 在角
在角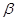 的终边上,且
的终边上,且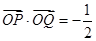 .
.
(1)求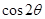 的值;
的值;
(2)求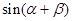 的值.
的值.
(本小题满分10分)在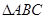 中,内角
中,内角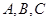 所对的边分别为
所对的边分别为 ,若
,若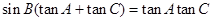 .
.
(1)求证: 成等比数列;
成等比数列;
(2)若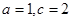 ,求
,求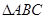 的面积
的面积 .
.
设不等式组 所表示的平面区域为Dn,记Dn内整点的个数为an(横纵坐标均为整数的点称为整点).
所表示的平面区域为Dn,记Dn内整点的个数为an(横纵坐标均为整数的点称为整点).
(1)n=2时,先在平面直角坐标系中作出区域D2,再求a2的值;
(2)求数列{an}的通项公式;
(3)记数列{an}的前n项的和为Sn,试证明:对任意n∈N*,
恒有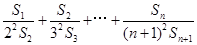 <
< 成立.
成立.
如图,已知双曲线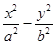 =1(a>0,b>0),定点
=1(a>0,b>0),定点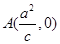 (c是双曲线的半焦距),双曲线虚轴的下端点为B.过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足
(c是双曲线的半焦距),双曲线虚轴的下端点为B.过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足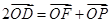 (O为原点),且
(O为原点),且 三点共线.
三点共线.
(1)求双曲线的离心率;
(2)若a=2,过点B的直线l交双曲线的左、右支于M、N两点,且△OMN的面积S△OMN=2 ,求l的方程.
,求l的方程.