 的三个内角
的三个内角 成等差数列,求证:
成等差数列,求证:
(本小题满分12分)
已知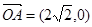 ,
, ,O为坐标原点,动点E满足:
,O为坐标原点,动点E满足:
(Ⅰ) 求点E的轨迹C的方程;
(Ⅱ)过曲线C上的动点P向圆O: 引两条切线PA、PB,切点分别为A、B,直线AB与x轴、y轴分别交于M、N两点,求ΔMON面积的最小值.
引两条切线PA、PB,切点分别为A、B,直线AB与x轴、y轴分别交于M、N两点,求ΔMON面积的最小值.
(本小题满分12分)
设函数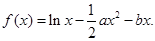
(Ⅰ) 当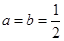 时,求函数
时,求函数 的最大值;
的最大值;
(Ⅱ)当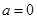 ,
,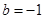 ,方程
,方程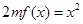 有唯一实数解,求正数
有唯一实数解,求正数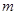 的值.
的值.
(本小题满分12分)
某校共有800名学生,高三一次月考之后,为了了解学生学习情况,用分层抽样方法从中抽出若干学生此次数学成绩,按成绩分组,制成如下的频率分布表:
| 组号 |
第 一 组 |
第 二 组 |
第 三 组 |
第 四 组 |
第 五 组 |
第 六 组 |
第 七 组 |
第 八 组 |
合计 |
| 分组 |
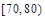 |
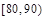 |
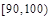 |
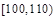 |
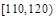 |
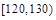 |
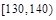 |
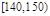 |
|
| 频数 |
4 |
6 |
20 |
22 |
18 |
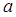 |
10 |
5 |
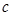 |
| 频率 |
0.04 |
0.06 |
0.20 |
0.22 |
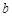 |
0.15 |
0.10 |
0.05 |
1 |
(Ⅰ)李明同学本次数学成绩为103分,求他被抽中的概率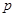 ;
;
(Ⅱ) 为了了解数学成绩在120分以上的学生的心理状态,现决定在第六、七、八组中用分层抽样方法抽取6名学生的成绩,并在这6名学生中在随机抽取2名由心理老师张老师负责面谈,求第七组至少有一名学生与张老师面谈的概率;
(Ⅲ) 估计该校本次考试的数学平均分。
(本小题满分12分)
如图:四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,平面PAD⊥平面ABCD,PA=BC=1,PD=AB=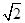 ,E、F分别为线段PD和BC的中点.
,E、F分别为线段PD和BC的中点.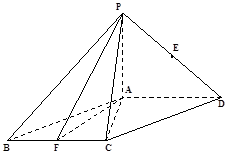
(Ⅰ)求证:CE∥平面PAF;
(Ⅱ) 在线段BC上是否存在一点G,使得平面PAG和平面PGC所成二面角的大小为60°?若存在,试确定G的位置;若不存在,请说明理由.
(本小题满分12分)已知数列 是等比数列,
是等比数列,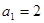 ,且
,且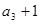 是
是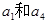 的等差中项.
的等差中项.
(Ⅰ) 求数列 的通项公式
的通项公式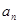 ;
;
(Ⅱ)若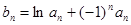 ,求数列
,求数列 的前n项和
的前n项和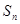 .
.