已知全集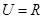 ,函数
,函数 的定义域为集合
的定义域为集合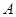 ,集合
,集合 =
= <
< <
<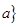 .
.
(1)求集合 ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围.
(本小题满分16分)
已知函数 是偶函数.
是偶函数.
(1)求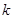 的值;
的值;
(2)设函数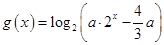 ,其中
,其中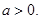 若函数
若函数 与
与 的图象有且只有一个交点,求
的图象有且只有一个交点,求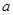 的取值范围.
的取值范围.
已知函数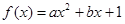 (
( ∈R且
∈R且 ),
),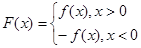 .
.
(Ⅰ)若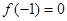 ,且函数
,且函数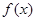 的值域为[0, +
的值域为[0, + ),求
),求 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的条件下,当x∈[-2 , 2 ]时,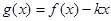 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;
(Ⅲ)设 ,
,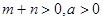 , 且
, 且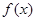 是偶函数,判断
是偶函数,判断 是否大于零?
是否大于零?
已知定义在实数集R上的函数y=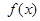 满足条件:对于任意实数x、y都有f(x+y)=f(x)+f(y).(1)求f(0);(2) 求证:
满足条件:对于任意实数x、y都有f(x+y)=f(x)+f(y).(1)求f(0);(2) 求证: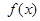 是奇函数;(3) 若
是奇函数;(3) 若 时,
时, ,求
,求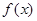 在
在 上的值域.
上的值域.
已知函数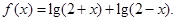
(1)求函数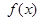 的定义域;
的定义域;
(2)记函数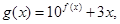 求函数
求函数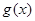 的值域.
的值域.