(本小题满分12分)
(1)已知 ,且
,且 为第三象限角,求
为第三象限角,求 的值;
的值;
(2)已知 ,计算
,计算 的值.
的值.
(本小题满分14分)
已知 为实数,数列
为实数,数列 满足
满足 ,当
,当 时,
时,
(1)当 时,求数列
时,求数列 的前100项的和
的前100项的和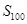 ;
;
(2)证明:对于数列 ,一定存在
,一定存在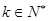 ,使
,使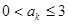 ;
;
(3)令 ,当
,当 时,求证:
时,求证:
(本小题满分14分)
已知函数 (
( 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线 平行.
平行.
(1)求实数 的取值范围;
的取值范围;
(2)是否存在实数 ,使得函数
,使得函数 的极小值为1,若存在,求出实数
的极小值为1,若存在,求出实数 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)设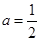 ,
, 的导数为
的导数为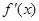 ,令
,令

求证:

(本小题满分14分)
已知圆 的方程为
的方程为 ,定直线
,定直线 的方程为
的方程为 .动圆
.动圆 与圆
与圆 外切,且与直线
外切,且与直线 相切.
相切.
(Ⅰ)求动圆圆心 的轨迹
的轨迹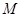 的方程;
的方程;
(II)斜率为 的直线
的直线 与轨迹
与轨迹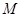 相切于第一象限的点
相切于第一象限的点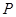 ,过点
,过点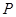 作直线
作直线 的垂线恰好经过点
的垂线恰好经过点 ,并交轨迹
,并交轨迹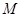 于异于点
于异于点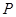 的点
的点 ,记
,记 为
为 (
( 为坐标原点)的面积,求
为坐标原点)的面积,求 的值.
的值.
(本小题满分14分)
设不等式 确定的平面区域为
确定的平面区域为 ,
, 确定的平面区域为
确定的平面区域为 .
.
(1)定义横、纵坐标为整数的点为“整点”,在区域 内任取3个整点,求这些整点中恰有2个整点在区域
内任取3个整点,求这些整点中恰有2个整点在区域 的概率;
的概率;
(2)在区域 内任取3个点,记这3个点在区域
内任取3个点,记这3个点在区域 的个数为
的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.