(本小题满分14分)
已知 为实数,数列
为实数,数列 满足
满足 ,当
,当 时,
时,
(1)当 时,求数列
时,求数列 的前100项的和
的前100项的和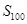 ;
;
(2)证明:对于数列 ,一定存在
,一定存在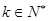 ,使
,使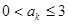 ;
;
(3)令 ,当
,当 时,求证:
时,求证:
一架飞以326km/h的速度,沿北偏东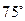 的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?
的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?
飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔20 250m,速度为1 000km/h,飞行员先看到山顶的俯角为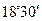 ,经过150 S后又看到山顶的俯角为
,经过150 S后又看到山顶的俯角为 ,求山顶的海拔高度(精确到1m).
,求山顶的海拔高度(精确到1m).
一个人在建筑物的正西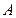 点,测得建筑物顶的仰角是
点,测得建筑物顶的仰角是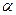 ,这个人再从
,这个人再从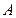 点向南走到
点向南走到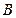 点,再测得建筑物顶的仰角是
点,再测得建筑物顶的仰角是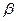 ,设
,设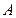 ,
,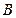 间的距离是
间的距离是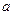 .
.
证明:建筑物的高是 .
.
测山上石油钻井的井架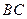 的高,从山脚
的高,从山脚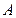 测得
测得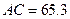 m,塔顶
m,塔顶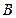 的仰角
的仰角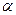 是
是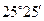 .已知山坡的倾斜角是
.已知山坡的倾斜角是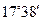 ,求井架的高
,求井架的高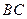 .
.
如图,货轮在海上以35n mile / h的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为 的方向航行.为了确定船位,在B点观察灯塔A的方位角是
的方向航行.为了确定船位,在B点观察灯塔A的方位角是 ,航行半小时后到达C点,观察灯塔A的方位角是
,航行半小时后到达C点,观察灯塔A的方位角是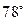 .求货轮到达C点时与灯塔A的距离(精确到1 n mile).
.求货轮到达C点时与灯塔A的距离(精确到1 n mile).
 |