(1)(2005全国卷1)已知椭圆的中心为坐标原点O,焦点在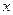 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,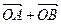 与
与 共线。(Ⅰ)求椭圆的离心率;(Ⅱ)设M为椭圆上任意一点,且
共线。(Ⅰ)求椭圆的离心率;(Ⅱ)设M为椭圆上任意一点,且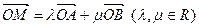 ,证明
,证明 为定值。
为定值。
(本小题满分12分)济南高新区引进一高科技企业,投入资金720万元建设基本设施,第一年各种运营费用120万元,以后每年增加40万元;每年企业销售收入500万元,设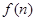 表示前
表示前 年的纯收入.(
年的纯收入.(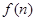 =前
=前 年的总收入-前
年的总收入-前 年的总支出-投资额)
年的总支出-投资额)
(Ⅰ)从第几年开始获取纯利润?
(Ⅱ)若干年后,该企业为开发新产品,有两种处理方案:
①年平均利润最大时,以480万元出售该企业;
②纯利润最大时,以160万元出售该企业;
问哪种方案最合算?
(本小题满分12分)已知定义在实数集 上的奇函数
上的奇函数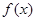 有最小正周期2,且当
有最小正周期2,且当 时,
时,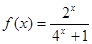
(Ⅰ)求函数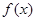 在
在 上的解析式;(Ⅱ)判断
上的解析式;(Ⅱ)判断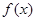 在
在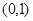 上的单调性;
上的单调性;
(Ⅲ)当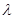 取何值时,方程
取何值时,方程 在
在 上有实数解?
上有实数解?
(本小题满分8分)已知平面向量a ,b
,b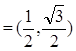
(Ⅰ)若存在实数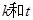 ,满足x
,满足x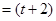 a
a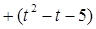 b,y
b,y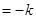 a
a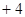 b且x⊥y,求出
b且x⊥y,求出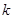 关于
关于 的关系式
的关系式 ;
;
(Ⅱ)根据(Ⅰ)的结论,试求出函数 在
在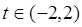 上的最小值.
上的最小值.
(本小题满分8分)设函数 的图象在
的图象在 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求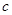 ,
,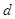 ;
;
(Ⅱ)若函数在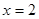 处取得极值
处取得极值 ,试求函数解析式并确定函数的单调区间.
,试求函数解析式并确定函数的单调区间.
(本小题满分8分)
已知 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足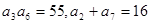 .
.
(Ⅰ)求数列 的通项公式:
的通项公式:
(Ⅱ)等比数列 满足:
满足: ,若数列
,若数列 ,求数列
,求数列 的前n项和
的前n项和 .
.