计算(1)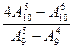 (2)
(2)
袋中有大小相同的红、黄两种颜色的球各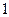 个,从中任取
个,从中任取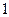 只,有放回地抽取
只,有放回地抽取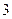 次.求:
次.求:
①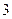 只全是红球的概率;
只全是红球的概率;
②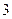 只颜色全相同的概率;
只颜色全相同的概率;
③ 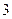 只颜色不全相同的概率.
只颜色不全相同的概率.
一个路口的红绿灯,红灯的时间为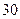 秒,黄灯的时间为
秒,黄灯的时间为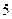 秒,绿灯的时间为
秒,绿灯的时间为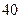 秒,当你到达路口时看见下列三种情况的概率各是多少?
秒,当你到达路口时看见下列三种情况的概率各是多少?
(1) 红灯 (2) 黄灯 (3)不是红灯
某路公共汽车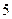 分钟一班准时到达某车站,求任一人在该车站等车时间少于
分钟一班准时到达某车站,求任一人在该车站等车时间少于 分钟的概率(假定车到来后每人都能上)
分钟的概率(假定车到来后每人都能上)
现有一批产品共有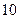 件,其中
件,其中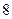 件为正品,
件为正品,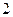 件为次品:
件为次品:
(1)如果从中取出一件,然后放回,再取一件,求连续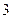 次取出的都是正品的概率;(2)如果从中一次取
次取出的都是正品的概率;(2)如果从中一次取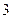 件,求
件,求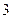 件都是正品的概率.
件都是正品的概率.
从甲、乙、丙、丁四个人中选两名代表,求:
(1)甲被选中的概率
(2)丁没被选中的概率