设集合W是满足下列两个条件的无穷数列{an}的集合:
① ②
② ,其中n∈N*,M是与n无关的常数
,其中n∈N*,M是与n无关的常数
(1)若{an}是等差数列,Sn是其前n项的和,a3=4,S3=18,试探究{Sn}与集合W之间的关系;
(2)设数列{bn}的通项为bn=5n-2n,且{bn}∈W,M的最小值为m,求m的值;
(3)在(2)的条件下,设 ,求证:数列{Cn}中任意不同的三项都不能成为等比数列.
,求证:数列{Cn}中任意不同的三项都不能成为等比数列.
如图,ABCD是边长为2的正方形,ABEF是矩形,且二面角C—AB—F是直二面角,AF=1,G是EF的中点.
(1)求证:平面AGC 平面BGC;
平面BGC;
(2)求GB与平面AGC所成角的正弦值.
如图,在正三棱柱ABC—A1B1C1中,底面边长为 ,D为BC中点,M在BB1上,且
,D为BC中点,M在BB1上,且
 .
.
(1)求证: ;
;
(2)求四面体 的体积.
的体积.
如图,在正方体ABCD—A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN//平面AA1B1B.
经过点 作直线l,若直线l与连接
作直线l,若直线l与连接 的线段总有公共点.
的线段总有公共点.
(1)求直线l斜率k的范围;
(2)直线l倾斜角 的范围;
的范围;
.已知 为常数,
为常数,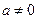 ,函数
,函数 ,
,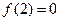 且方程
且方程 有等根.
有等根.
(1)求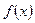 的解析式及值域;
的解析式及值域;
(2)设集合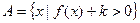 ,
,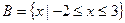 ,若
,若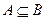 ,求实数
,求实数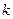 的取值范围;
的取值范围;
(3)是否存在实数 ,使
,使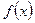 的定义域和值域分别为
的定义域和值域分别为 和
和 ?若存在,求出
?若存在,求出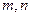 的值;若不存在,说明理由.
的值;若不存在,说明理由.