 个人坐在一排
个人坐在一排 个座位上,问(1)空位不相邻的坐法有多少种?(2)
个座位上,问(1)空位不相邻的坐法有多少种?(2)  个空位只有
个空位只有 个相邻的坐法有多少种?(3)
个相邻的坐法有多少种?(3)  个空位至多有
个空位至多有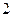 个相邻的坐法有多少种?
个相邻的坐法有多少种?
将3个完全相同的小球随机地放入编号依次为1,2,3,4,5的盒子里,用随机变量 表示有球盒子编号的最大值.
表示有球盒子编号的最大值.
(Ⅰ)求 ;
;
(Ⅱ)求 的分布列和数学期望
的分布列和数学期望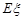 .
.
已知函数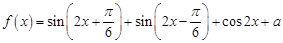 (
(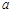 为常数)的最大值是3.
为常数)的最大值是3.
(Ⅰ)求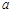 的值;
的值;
(Ⅱ)在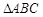 中,
中,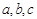 分别是角
分别是角 的对边,
的对边, ,求
,求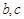 的值.
的值.
某单位为绿化环境,移栽了甲、乙两种大树各2株。设甲、乙两种大树移栽的成活率分别为
和
,且各株大树是否成活互不影响。求移栽的4株大树中:
(Ⅰ)至少有1株成活的概率;
(Ⅱ)两种大树各成活1株的概率。
(本小题满分12分)已知定义在 上的两个函数
上的两个函数 的图象在点
的图象在点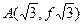 处的切线倾斜角的大小为
处的切线倾斜角的大小为 (1)求
(1)求 的解析式;(2)试求实数k的最大值,使得对任意
的解析式;(2)试求实数k的最大值,使得对任意 恒成立;(3)若
恒成立;(3)若
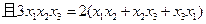 ,求证:
,求证:
(本小题满分13分)重庆、成都两个现代化城市之间有7条网线并联,这7条网线能通过的信息量分别为1,1,2,2,2,3,3(信息流量单位),现从中任选三条网线,设可通过的信息量为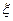 。若可通过的信息量
。若可通过的信息量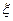 ≥6,则可保证信息通畅。(1)求线路信息通畅的概率;(2)求线路可通过的信息量
≥6,则可保证信息通畅。(1)求线路信息通畅的概率;(2)求线路可通过的信息量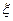 的分布列和数学期望。
的分布列和数学期望。
网