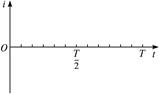
如图所示,abcd为一个闭合矩形金属线框,图中虚线为磁场右边界(磁场的左边界很远),它与线圈的ab边平行,等分bc边,即线圈有一半位于匀强磁场之中,而另一半位于磁场之外,磁感线方向垂直于线框平面向里.线框以ab边为轴匀速转动,t=0时刻线圈的位置如图所示.在下面的坐标系中定性画出转动过程中线圈内感应电流随时间变化的图象(只要求画出一个周期).
如图9所示，宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度v0抛出一个小球，测得小球经时间t落到斜坡上另一点Q，斜面倾角为α，已知星球半径为R，万有引力常量为G，求：
（1）该星球表面的重力加速度g
（2）该星球的密度ρ
（3）该星球的第一宇宙速度v
以速度v0平抛一个质量为1kg的物体，若在抛出3s后它未与地面及其他物体相碰，求它在3s内动量的变化。
一个质量为m=10kg的物体静止在水平地面上，若以F=60N的水平拉力作用在物体上，使物体沿地面运动5s后再将拉力撤去，求撤去拉力后物体再运动几秒钟停下来？（已知物体与水平地面间的动摩擦因数为0.2）
如图所示，滑块以某一速率靠惯性沿固定斜面由底端A向上运动，到达最高点B时离地面的高度为H，然后又沿斜面返回，到出发点A时的速率为原来速率的一半。若取斜面底端重力势能为零，求上升过程中滑块动能等于势能的位置离地面的高度h。
在一次抗洪抢险活动中，解放军某部运用直升机抢救一重要落水物体，在静止在空中的直升机上用电动机通过悬绳将物体从离飞机90m处的洪水中吊到机舱里，已知物体的质量为80kg，吊绳的拉力不能超过1200N，电动机的额定输出功率为12kW，为尽快把物体安全救起，操作人员采取的办法是：先让吊绳以最大的拉力工作一段时间，达额定功率后电动机以额定功率工作，当物体到达机舱时它达到最大速度。（g=10m/s2）
求：（1）落水物体刚到达机舱时的速度；
（2）这一过程所用的时间。